Simetría molecular para niños
En química, la simetría molecular es como la forma o el diseño de una molécula. Nos ayuda a entender cómo se ven las moléculas en el espacio y cómo se comportan. Imagina que una molécula es como un objeto que puedes girar o reflejar. Si después de hacer eso, la molécula se ve exactamente igual que antes, decimos que tiene simetría.
Conocer la simetría de una molécula es muy importante. Nos ayuda a predecir muchas de sus características, como si tiene un lado positivo y uno negativo (su momento dipolar) o cómo interactúa con la luz. Para estudiar la simetría molecular, los científicos usan una herramienta matemática llamada teoría de grupos. También hay formas de descubrir la simetría de una molécula en un laboratorio, como usando cristalografía de rayos X o diferentes tipos de espectroscopia.
Contenido
Elementos de Simetría: Las Piezas Clave
La simetría de una molécula se describe usando cinco tipos de "elementos de simetría". Piensa en ellos como las reglas que nos dicen si una molécula es simétrica.
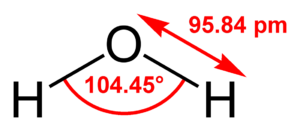
- El eje de simetría (Cn) es una línea imaginaria alrededor de la cual puedes girar una molécula. Si la giras un cierto número de grados (360° dividido por 'n') y se ve igual que al principio, entonces tiene un eje de simetría. Por ejemplo, la molécula de agua tiene un eje C2 (puedes girarla 180° y se ve igual). La molécula de amoníaco tiene un eje C3 (gira 120°). Si una molécula tiene varios ejes, el que permite el giro más pequeño (el 'n' más alto) se llama eje principal.
- El plano de simetría o plano espejo (σ) es como un espejo imaginario que divide la molécula. Si reflejas la molécula a través de este plano y obtienes una copia idéntica a la original, entonces tiene un plano de simetría. La molécula de agua tiene dos planos de simetría.
- El centro de simetría (i) es un punto en el centro de la molécula. Si desde cualquier átomo de la molécula trazas una línea recta a través de este punto, encontrarás otro átomo idéntico a la misma distancia del centro.
- El eje de rotación-reflexión (Sn) es una combinación de dos movimientos. Primero, giras la molécula alrededor de un eje (como en el eje de simetría). Luego, la reflejas en un plano que es perpendicular a ese eje. Si la molécula se ve igual después de estos dos pasos, tiene un eje de rotación-reflexión.
- La identidad (E) es el elemento de simetría más simple. Significa que la molécula no cambia en absoluto. Todas las moléculas tienen este elemento, aunque parezca obvio, es importante para la teoría de grupos.
Operaciones de Simetría: Los Movimientos
Una operación de simetría es el movimiento que realizas sobre una molécula para que se vea igual que antes. Cada elemento de simetría tiene una o más operaciones asociadas. Por ejemplo, girar una molécula alrededor de un eje es una operación (Ĉn), y no hacer nada es la operación de identidad (Ê). Algunas operaciones son equivalentes a otras más complejas, lo que simplifica su estudio.
Grupos Puntuales: Clasificando la Simetría
Un grupo puntual es un conjunto de todas las operaciones de simetría que una molécula puede tener, y que dejan al menos un punto de la molécula en el mismo lugar. En el mundo tridimensional, hay 32 tipos de grupos puntuales, y 30 de ellos son importantes para entender las moléculas en química.
La Teoría de Grupos en Acción
La teoría de grupos es una rama de las matemáticas que nos ayuda a organizar y entender las operaciones de simetría. Un "grupo" de operaciones de simetría debe cumplir cuatro reglas:
- Si haces dos operaciones de simetría seguidas, el resultado debe ser otra operación que también pertenezca al grupo (esto se llama "cierre").
- El orden en que haces las operaciones no importa si las agrupas de cierta manera (es "asociativa").
- El grupo siempre debe incluir la operación de identidad (E), que significa no hacer nada.
- Para cada operación en el grupo, debe haber otra operación que la "deshaga" y te devuelva al estado original (esto se llama "elemento inverso").
El "orden" de un grupo es simplemente el número total de operaciones de simetría que tiene.
Por ejemplo, la molécula de agua pertenece al grupo puntual C2v. Sus operaciones de simetría son: la identidad (E), una rotación de 180° (C2), y dos reflexiones en planos diferentes (σv y σv'). El orden de este grupo es 4, porque tiene 4 operaciones. Si giras la molécula de agua 180° (C2) y luego la reflejas en uno de sus planos (σv), obtendrás el mismo resultado que si hubieras hecho la otra reflexión (σv').
Tablas de Caracteres: El Mapa de la Simetría
Para cada grupo puntual, existe una "tabla de caracteres". Esta tabla es como un mapa que resume toda la información sobre las operaciones de simetría y cómo se comportan las diferentes partes de una molécula bajo esas operaciones.
Las tablas de caracteres nos dicen cómo una parte específica de la molécula (como un orbital atómico, que es el espacio donde se encuentran los electrones) se transforma cuando aplicamos una operación de simetría. Los valores en la tabla suelen ser 1 o -1:
- Un 1 significa que la parte de la molécula no cambia de signo o dirección (es simétrica).
- Un -1 significa que cambia de signo o dirección (es asimétrica).
Las representaciones en la tabla tienen nombres especiales:
- A se usa cuando la rotación alrededor del eje principal es simétrica.
- B se usa cuando la rotación alrededor del eje principal es asimétrica.
- E y T se usan para representaciones más complejas.
- Si el grupo puntual tiene un centro de simetría, se usan los subíndices 'g' (de "gerade", que significa "par" en alemán) si no hay cambio de signo, y 'u' (de "ungerade", que significa "impar") si hay cambio de signo.
La tabla de caracteres para el grupo C2v (el del agua) se ve así:
| C2v | E | C2 | σv(xz) | σv'(yz) | ||
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | −1 | −1 | Rz | xy |
| B1 | 1 | −1 | 1 | −1 | x, Ry | xz |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
En esta tabla, las letras A, B, E, T son las "representaciones irreducibles". Las columnas muestran cómo se comporta cada representación bajo las operaciones de simetría (E, C2, σv, σv'). Las últimas columnas nos dicen qué tipos de orbitales o movimientos tienen esa misma simetría. Por ejemplo, el orbital 2px del agua tiene la simetría de la representación B1, porque su comportamiento bajo las operaciones de simetría es {1, -1, 1, -1}.
Un Poco de Historia
Los científicos han estudiado la simetría molecular por mucho tiempo. Hans Bethe fue uno de los primeros en usar las ideas de los grupos puntuales en 1929 para entender cómo los átomos se unen en las moléculas. Luego, Eugene Wigner usó la teoría de grupos para explicar cómo vibran las moléculas. La primera tabla de caracteres completa fue creada por László Tisza en 1933. Estos estudios han sido fundamentales para el desarrollo de la química moderna.
Véase también
 En inglés: Molecular symmetry Facts for Kids
En inglés: Molecular symmetry Facts for Kids

