Semejanza (geometría) para niños
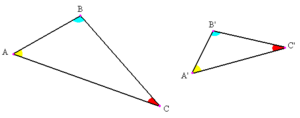
En geometría euclidiana, dos figuras geométricas son semejantes si tienen la misma forma, aunque su tamaño sea diferente. Imagina que tienes una foto y la amplías o la reduces; la nueva foto es semejante a la original porque la forma no cambia, solo el tamaño.
Si dos figuras son semejantes, una se puede obtener de la otra haciendo una de estas cosas o una combinación de ellas:
- Agrandar o reducir: Cambiar su tamaño de forma uniforme.
- Mover: Desplazarla de un lugar a otro sin girarla ni cambiar su tamaño.
- Girar: Rotarla alrededor de un punto.
- Reflejar: Como si la vieras en un espejo.
Por ejemplo, todos los círculos son semejantes entre sí, sin importar su tamaño. Lo mismo ocurre con todos los cuadrados y todos los triángulos equiláteros. Sin embargo, no todas las elipses son semejantes, ni todos los rectángulos, ni todos los triángulos isósceles. Esto es porque pueden tener proporciones diferentes.
Dos triángulos que son exactamente iguales (llamados congruentes) también se consideran semejantes, con una razón de proporción de 1.
Contenido
¿Qué es la semejanza en geometría?
Decimos que dos figuras son semejantes si la distancia entre dos puntos cualquiera de la primera figura, dividida por la distancia entre los puntos correspondientes en la segunda figura, siempre da el mismo número. Este número se llama la razón de semejanza o factor de escala.
Propiedades de los triángulos semejantes
Para indicar que dos triángulos son semejantes, usamos un símbolo especial: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bigtriangleup ABC\sim\bigtriangleup A'B'C' . Esto significa que el triángulo ABC es semejante al triángulo A'B'C'.
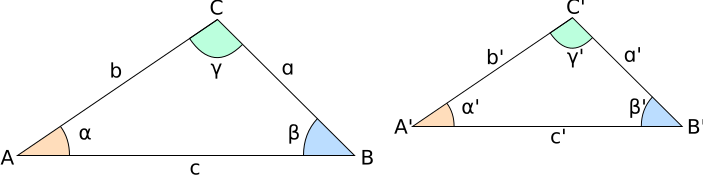
Dos triángulos son semejantes si cumplen dos condiciones importantes:
- Sus ángulos correspondientes son iguales. Por ejemplo, si el ángulo A es igual al ángulo A', el ángulo B al B', y el ángulo C al C'.
- Sus lados correspondientes son proporcionales. Esto significa que si divides la longitud de un lado del primer triángulo entre la longitud del lado correspondiente del segundo triángulo, siempre obtendrás el mismo número (la razón de semejanza).
Si se cumple una de estas condiciones, la otra también se cumple automáticamente.
La semejanza tiene algunas propiedades interesantes:
- Propiedad reflexiva: Cualquier triángulo es semejante a sí mismo. Es como mirarse en un espejo.
- Propiedad simétrica: Si un triángulo es semejante a otro, entonces el segundo triángulo también es semejante al primero.
- Propiedad transitiva: Si el triángulo A es semejante al triángulo B, y el triángulo B es semejante al triángulo C, entonces el triángulo A también es semejante al triángulo C.
Teorema fundamental de la semejanza de triángulos
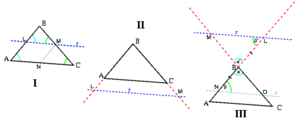
Este teorema es muy útil para entender la semejanza. Dice que si dibujas una línea paralela a uno de los lados de un triángulo, esa línea crea un triángulo más pequeño que es semejante al triángulo original.
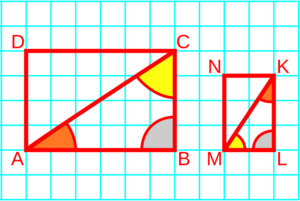
Imagina un triángulo grande ABC. Si trazas una línea recta que sea paralela al lado AC y que corte los otros dos lados (AB y BC), esta línea formará un nuevo triángulo más pequeño, por ejemplo, BLM. Este nuevo triángulo BLM será semejante al triángulo original BAC.
Esto ocurre porque los ángulos del triángulo pequeño son iguales a los ángulos del triángulo grande. Por ejemplo, el ángulo B es común a ambos triángulos, y los otros ángulos son iguales porque son ángulos correspondientes entre líneas paralelas. Además, los lados del triángulo pequeño serán proporcionales a los lados del triángulo grande.
Semejanza en el espacio tridimensional
El concepto de semejanza no solo se aplica a figuras planas, sino también a objetos en el espacio tridimensional. Por ejemplo, una maqueta de un edificio es semejante al edificio real. La maqueta es una versión a escala del edificio.
En el espacio, una semejanza es una transformación que multiplica todas las distancias por el mismo número positivo, llamado la razón de semejanza. Si la razón de semejanza es 1, entonces la figura no cambia de tamaño, solo se mueve o gira, lo que se llama una isometría.
Las semejanzas mantienen la forma de los objetos, conservando propiedades como el paralelismo, la perpendicularidad y los ángulos.
Relación entre áreas y volúmenes de figuras semejantes
Cuando dos figuras son semejantes, la relación entre sus áreas y volúmenes sigue reglas especiales:
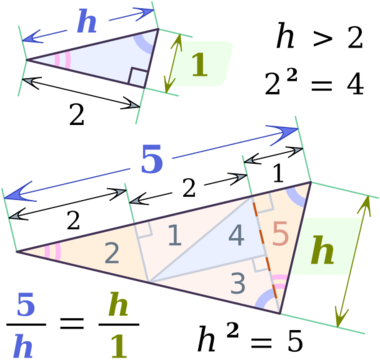
- Áreas: La razón entre las áreas de dos figuras semejantes es igual al cuadrado de la razón de semejanza de sus lados. Por ejemplo, si un cuadrado tiene un lado de 2 cm y otro cuadrado semejante tiene un lado de 4 cm (el doble, razón de semejanza = 2), su área será 2 al cuadrado (4) veces mayor. Si el primer cuadrado tiene un área de 4 cm², el segundo tendrá 16 cm².
- Volúmenes: La razón entre los volúmenes de dos figuras semejantes es igual al cubo de la razón de semejanza de sus lados. Por ejemplo, si un cubo tiene un lado de 2 cm y otro cubo semejante tiene un lado de 4 cm (razón de semejanza = 2), su volumen será 2 al cubo (8) veces mayor. Si el primer cubo tiene un volumen de 8 cm³, el segundo tendrá 64 cm³.
Esta relación es muy importante en campos como la ingeniería y la biología, y se conoce como la Ley Cuadrático-Cúbica.
Semejanza en otras geometrías
La idea de que una figura puede agrandarse o reducirse sin cambiar su forma es muy natural en la geometría que estudiamos normalmente (geometría euclidiana). Sin embargo, los matemáticos descubrieron que esto no siempre es así en otros tipos de geometrías, llamadas geometrías no euclidianas.
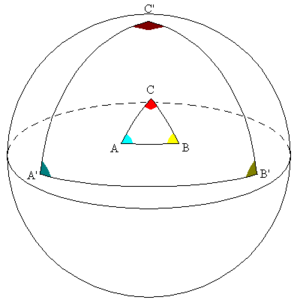
Por ejemplo, en la geometría de una esfera (como la superficie de la Tierra), si dibujas un triángulo y luego intentas "agrandarlo" manteniendo la misma forma, verás que sus ángulos cambian. Esto significa que la semejanza se comporta de manera diferente en espacios curvos. En la geometría euclidiana, los triángulos semejantes tienen los mismos ángulos y lados proporcionales, pero en una esfera, un triángulo "agrandado" tendrá ángulos diferentes.
Otros polígonos semejantes
El concepto de semejanza se aplica a cualquier polígono, no solo a los triángulos. Dos polígonos son semejantes si:
- Sus lados correspondientes son proporcionales.
- Sus ángulos correspondientes son iguales.
Es importante que se cumplan ambas condiciones. Por ejemplo, no todos los rombos son semejantes (aunque sus lados sean proporcionales, sus ángulos pueden ser diferentes), ni todos los rectángulos (aunque sus ángulos sean todos de 90 grados, sus lados pueden no ser proporcionales).
Una condición suficiente para que dos polígonos sean semejantes es que tanto sus lados como sus diagonales correspondientes sean proporcionales.
Un dato interesante es que todos los polígonos regulares con el mismo número de lados son semejantes entre sí. Por ejemplo, todos los cuadrados son semejantes, y todos los pentágonos regulares son semejantes.
Véase también
 En inglés: Similarity (geometry) Facts for Kids
En inglés: Similarity (geometry) Facts for Kids
- Triángulo
- Congruencia de triángulos
- Teorema de Tales
- Teorema de Pitágoras
- Proporcionalidad