Símplex para niños

En geometría, un símplex (también llamado n-símplex o símplice) es como una versión de un triángulo pero en diferentes dimensiones. Imagina un triángulo, que tiene 2 dimensiones. Un símplex es la forma que se crea al unir un grupo de puntos de una manera especial en un espacio. Estos puntos deben estar colocados de forma que no todos estén en la misma línea o plano.
Por ejemplo:
- Un 0-símplex es solo un punto.
- Un 1-símplex es un segmento de una línea (como un palo).
- Un 2-símplex es un triángulo (con su interior).
- Un 3-símplex es un tetraedro (una pirámide de cuatro caras, con su interior).
- Un 4-símplex es una figura más compleja llamada pentácoron (también con su interior).
Un símplex regular es una forma geométrica perfecta, como un politopo regular. Puedes construir un símplex regular de una dimensión más alta añadiendo un nuevo punto y conectándolo a todos los puntos anteriores con líneas del mismo tamaño.
Cuando tomas algunos de los puntos que forman un símplex, la forma que crean también es un símplex más pequeño. A estas partes se les llama "caras".
- Las 0-caras son los puntos, llamados vértices.
- Las 1-caras son las líneas, llamadas lados.
- Las (n-1)-caras son las superficies más grandes, llamadas facetas.
- La única n-cara es el símplex completo.
El número de caras de un símplex se puede encontrar usando el Triángulo de Pascal, una tabla numérica muy interesante.
¿Qué es el Símplex Estándar?
El n-símplex estándar es una versión especial de un símplex que se usa como referencia. Se define en un espacio matemático llamado Rn+1. Imagina que tienes un conjunto de números (t0, t1, ..., tn). Para que estos números formen un símplex estándar, deben cumplir dos reglas:
- La suma de todos los números debe ser igual a 1.
- Cada número debe ser mayor o igual a cero.
Los puntos principales de este símplex estándar se llaman vértices. Son puntos donde solo uno de los números es 1 y los demás son 0. Por ejemplo, para un 2-símplex estándar, los vértices serían (1,0,0), (0,1,0) y (0,0,1).
Estos números (ti) se conocen como coordenadas baricéntricas. Son como "pesos" que te dicen dónde está un punto dentro del símplex.
¿Cómo se calcula el volumen de un símplex?
Calcular el volumen de un símplex puede ser un poco complicado, pero hay una fórmula para ello. Si conoces las coordenadas de todos los puntos que forman el símplex, puedes usar una fórmula especial que involucra algo llamado determinantes de Cayley-Menger.
Para un n-símplex con n+1 vértices (puntos), el volumen se calcula con una fórmula que usa una tabla de números llamada matriz. Esta fórmula es:
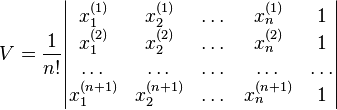
Donde V es el volumen, n! es el factorial de n (por ejemplo, 3! = 3x2x1), y la tabla con las barras verticales es un determinante que se calcula con las coordenadas de los vértices.
Véase también
 En inglés: Simplex Facts for Kids
En inglés: Simplex Facts for Kids
- Politopo
- Algoritmo símplex
- Método Nelder-Mead


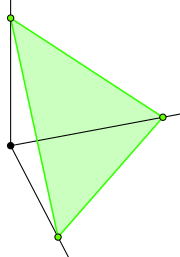
 es un triángulo en el espacio
es un triángulo en el espacio