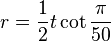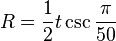Pentacontágono para niños
Datos para niños Pentacontágono |
||
|---|---|---|
 Un pentacontágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 50540), orden 2×50 | |
| Vértices | 50 | |
| Símbolo de Schläfli | {50} t{25} (pentacontágono regular) | |
| Diagrama de Coxeter-Dynkin |      |
|
| Polígono dual | Autodual | |
| Área | 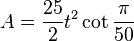 (lado  ) |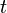
|
| Ángulo interior | 172.8° | |
| Propiedades | ||
| Convexo, isogonal, cíclico, equilateral, isotoxal | ||
En geometría, un pentacontágono (también llamado pentecontágono o 50-gono) es una figura plana que tiene cincuenta lados rectos y cincuenta vértices (puntos donde se unen los lados).
La suma de todos los ángulos interiores de cualquier pentacontágono siempre es de 8640 grados.
Contenido
Pentacontágono: Un Polígono de 50 Lados
Un pentacontágono es un tipo de polígono, que son figuras geométricas cerradas formadas por segmentos de línea recta. Lo que hace especial al pentacontágono es su gran número de lados: ¡cincuenta!
Características de un Pentacontágono Regular
Un pentacontágono se considera "regular" cuando todos sus lados tienen la misma longitud y todos sus ángulos interiores son iguales.
Ángulos Interiores y Exteriores
En un pentacontágono regular, cada ángulo interior mide 172.8 grados. Esto significa que está muy cerca de ser una línea recta, lo que hace que la figura se vea casi como un círculo.
El ángulo exterior de un pentacontágono regular es de 7.2 grados. Los ángulos exteriores son los que se forman al extender uno de los lados del polígono.
Cómo Calcular su Área
Para calcular el área de un pentacontágono regular, se usa una fórmula matemática. Si t es la longitud de uno de sus lados, el área (A) se calcula así:
También podemos calcular el inradio (r), que es el radio de la circunferencia más grande que puede dibujarse dentro del polígono y tocar todos sus lados:
Y el circunradio (R), que es el radio de la circunferencia que pasa por todos los vértices del polígono:
¿Se Puede Construir con Regla y Compás?
Un pentacontágono regular no se puede dibujar usando solo una regla y compás. Esto se debe a que el número 50 (que es 2 × 52) no cumple con ciertas condiciones matemáticas para ser construible de esa manera.
Sin embargo, sí se puede construir usando herramientas adicionales llamadas "curvas auxiliares". Estas curvas, como la Cuadratriz de Hipias o una espiral de Arquímedes, permiten dividir ángulos en partes iguales. Por ejemplo, se puede dibujar un ángulo de 36 grados con regla y compás, y luego dividirlo en cinco partes iguales usando una espiral de Arquímedes. Esto nos daría el ángulo de 7.2 grados necesario para construir un pentacontágono.
Simetría en los Pentacontágonos
La simetría es cuando una figura se ve igual después de girarla o reflejarla. Un pentacontágono regular tiene una simetría muy alta, llamada simetría diedral Dih50. Esto significa que tiene 50 ejes de reflexión (líneas por las que se puede doblar y las dos mitades coinciden) y puede girarse de 50 maneras diferentes y seguir viéndose igual.
Existen diferentes tipos de simetrías más simples que también se pueden encontrar en pentacontágonos que no son perfectamente regulares. El matemático John Horton Conway usó letras para describir estas simetrías:
- d (diagonal): Ejes de simetría que pasan por los vértices.
- p (perpendicular): Ejes de simetría que pasan por el centro de los lados.
- i (invertida): Ejes de simetría que pasan por vértices y lados.
- g (giro): Simetría de rotación.
- a1: No tiene simetría.
Pentacontagramas: Estrellas de 50 Puntas
Un pentacontagrama es una estrella que tiene 50 puntas o vértices. Se forman conectando los vértices de un pentacontágono regular de una manera específica, saltándose algunos vértices.
Hay varias formas de pentacontagramas regulares, cada una con un Símbolo de Schläfli diferente, como {50/3}, {50/7}, {50/9}, {50/11}, {50/13}, {50/17}, {50/19}, {50/21} y {50/23}. El número después de la barra indica cuántos vértices se saltan al dibujar la estrella.
| Imagen |  {50⁄3} |
 {50⁄7} |
 {50⁄9} |
 {50⁄11} |
 50⁄13 |
|---|---|---|---|---|---|
| ángulo interior | 158.4° | 129.6° | 115.2° | 100.8° | 86.4° |
| Imagen |  {50⁄17 } |
 {50⁄19 } |
 {50⁄21 } |
 {50⁄23 } |
|
| ángulo interior | 57.6° | 43.2° | 28.8° | 14.4° |
Galería de imágenes
-
Simetrías de un pentacontágono regular. Las líneas de color azul claro muestran subgrupos del índice 2. Los 3 subgrafos encuadrados están relacionados posicionalmente por subgrupos de índice 5.
Véase también
En inglés: Pentacontagon Facts for Kids
