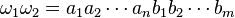Palabra (matemáticas) para niños
En matemáticas, una palabra es como una secuencia ordenada de letras o símbolos que tomamos de un grupo fijo llamado alfabeto.
Por ejemplo, si nuestro alfabeto es X={a,e,i,o,u}, que son las vocales, entonces las siguientes son ejemplos de palabras que podemos formar:
- aeo
- ioi
- aeaeoa
- uuuu
La cantidad de símbolos que tiene una palabra se llama su longitud.
Contenido
¿Qué es una palabra en matemáticas?
Definición de una palabra y sus símbolos
Una palabra se define así: si tenemos un conjunto A, al que llamamos alfabeto, una palabra sobre el alfabeto A es una secuencia de símbolos como 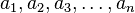 . Cada uno de estos símbolos (
. Cada uno de estos símbolos (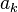 ) debe ser parte del alfabeto A.
) debe ser parte del alfabeto A.
Aunque se definen como secuencias, es común escribir los símbolos juntos, sin comas. A los elementos del alfabeto también se les llama símbolos del alfabeto.
Si una palabra es 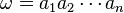 sobre un alfabeto A, el número n es la longitud de la palabra y se escribe
sobre un alfabeto A, el número n es la longitud de la palabra y se escribe 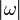 . Una palabra con longitud n se llama una n-palabra.
. Una palabra con longitud n se llama una n-palabra.
La palabra vacía: una palabra especial
Para cualquier alfabeto, existe una palabra de longitud cero. Esta se llama la palabra vacía y se representa con "" o 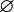 . Es como una palabra que no tiene ningún símbolo.
. Es como una palabra que no tiene ningún símbolo.
Palabras binarias: solo ceros y unos
Cuando un alfabeto tiene solo dos elementos, las palabras que se forman se llaman palabras binarias. Generalmente, para estas palabras se usa el alfabeto A={0, 1}.
Palíndromos: palabras que se leen igual al revés
Si tenemos una palabra 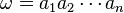 , su palabra inversa es
, su palabra inversa es 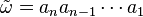 . Una palabra
. Una palabra 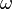 es un palíndromo si es igual a su palabra inversa, es decir,
es un palíndromo si es igual a su palabra inversa, es decir,  . Por ejemplo, "oso" o "reconocer" son palíndromos.
. Por ejemplo, "oso" o "reconocer" son palíndromos.
¿Cómo se usan las palabras para contar?
Combinatoria: contando posibilidades con palabras
Las palabras son muy importantes en un área de las matemáticas llamada combinatoria enumerativa. Nos ayudan a contar cuántas formas hay de organizar cosas. Esto se debe a que muchos problemas de conteo se pueden convertir en problemas de contar palabras que cumplen ciertas reglas.
Regla básica para contar palabras
Un resultado fundamental es este:
|
Esto es porque para crear una palabra, tienes que elegir un símbolo para cada una de las n posiciones. Si en cada posición tienes r opciones, entonces el número total de combinaciones es r multiplicado por sí mismo n veces, lo que es rn.
Ejemplo: Contando subconjuntos con palabras binarias
Aquí tienes un ejemplo clásico de cómo las palabras nos ayudan a contar:
|
| Demostración |
Imagina que tienes un conjunto X con n elementos, por ejemplo, 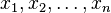 . .
Ahora, cada subconjunto de X (un grupo de elementos de X) se puede representar con una palabra binaria (usando solo 0 y 1). La regla es la siguiente:
Por ejemplo, si el conjunto es
De la misma manera, cualquier palabra binaria de longitud n representa un subconjunto de X. Así, el número de subconjuntos es igual al número de palabras binarias de longitud n. Como ya vimos, el número de palabras de longitud n sobre un alfabeto con dos símbolos (0 y 1) es |
¿Cómo se relacionan las palabras entre sí?
Estructura algebraica: uniendo palabras
Para cualquier alfabeto A, podemos unir palabras usando una operación llamada concatenación.
|
Esto significa que simplemente pones una palabra después de la otra. Por ejemplo, si tienes "hola" y "mundo", su concatenación es "holamundo".
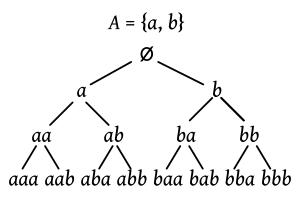
La longitud de una palabra que resulta de la concatenación es la suma de las longitudes de las palabras originales: 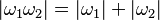 .
.
La concatenación es una operación que cumple ciertas reglas matemáticas. Por ejemplo, es asociativa (no importa cómo agrupes las palabras al unirlas) y la palabra vacía actúa como un elemento neutro (si la unes a otra palabra, la otra palabra no cambia). Por estas propiedades, el conjunto de todas las palabras sobre un alfabeto forma una estructura matemática llamada monoide libre.
Partes de una palabra: factores, prefijos y sufijos
Una palabra  es un factor de otra palabra
es un factor de otra palabra 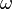 si
si  aparece dentro de
aparece dentro de 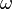 . Por ejemplo, "ola" es un factor de "hola".
. Por ejemplo, "ola" es un factor de "hola".
Si el factor  está al principio de la palabra
está al principio de la palabra 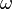 , se llama prefijo. Por ejemplo, "ho" es un prefijo de "hola". Si el factor
, se llama prefijo. Por ejemplo, "ho" es un prefijo de "hola". Si el factor  está al final de la palabra
está al final de la palabra 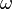 , se llama sufijo. Por ejemplo, "ola" es un sufijo de "hola".
, se llama sufijo. Por ejemplo, "ola" es un sufijo de "hola".
Lenguajes formales: reglas para las palabras
En los lenguajes formales, que son conjuntos de palabras que siguen ciertas reglas, el alfabeto es el conjunto de todos los símbolos que se usan. Algunos lenguajes pueden usar alfabetos con muchos símbolos, o incluso palabras infinitas.
Por ejemplo, el lenguaje de la lógica de primer orden usa un alfabeto que incluye símbolos para conectar ideas (como "y", "o"), para cuantificar (como "para todo", "existe"), muchas variables, el símbolo de igualdad '=', y paréntesis. También puede tener símbolos para constantes, funciones y relaciones.
Las palabras y los alfabetos también son muy importantes en la teoría de autómatas, que estudia máquinas abstractas y cómo procesan información.
Palabras en la computación
Cadena de caracteres: palabras en la informática
En las ciencias de la computación, el concepto de palabra es muy similar al de cadena de caracteres. Una cadena de caracteres es una secuencia de símbolos o unidades de información, y es uno de los tipos de datos más básicos que se usan en programación.
En computación, los elementos de las cadenas suelen ser bytes que forman un arreglo. Estos bytes representan información usando un código especial. En cambio, en matemáticas, los elementos del alfabeto pueden ser cualquier cosa, incluso otros conjuntos, y no tienen restricciones de cómo se representan.
Palabras binarias en computación
Queremos saber cuántas palabras binarias de longitud n existen. Es decir, cuántas secuencias de n símbolos formadas solo por 0s y 1s podemos crear. Por ejemplo, las palabras binarias de longitud 4 son:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Es importante saber que una palabra binaria no es lo mismo que un número binario. Una palabra binaria es solo una lista de símbolos. Por ejemplo, las palabras 0010, 010 y 10 son diferentes como palabras, aunque todas se puedan interpretar como el número binario 10.
Para elegir una palabra binaria de longitud n, tenemos que tomar n decisiones. Para la primera posición, podemos elegir 0 o 1 (2 opciones). Para la segunda posición, también tenemos 2 opciones, y así sucesivamente para cada una de las n posiciones.
Cada serie de n elecciones crea una palabra, y cada palabra corresponde a n elecciones. Por lo tanto, el número de palabras binarias es igual al número de formas de hacer n elecciones, donde cada elección tiene 2 posibilidades. El principio del producto nos dice que el resultado es 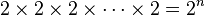 .
.
De manera similar, si queremos contar palabras de longitud n donde cada posición puede ser cualquiera de r símbolos posibles, el número total de formas de hacerlo será 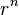 .
.
Galería de imágenes
-
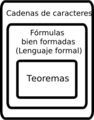
Esta imagen muestra la relación entre las cadenas de caracteres, las fórmulas bien formadas y los teoremas. En algunos sistemas formales, sin embargo, el conjunto de los teoremas coincide con el de las fórmulas bien formadas.


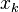 está en el subconjunto, y tiene un 0 si no lo está.
está en el subconjunto, y tiene un 0 si no lo está.
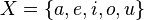 , y queremos representar el subconjunto S={a,o,u}, la palabra binaria sería 10011:
, y queremos representar el subconjunto S={a,o,u}, la palabra binaria sería 10011: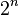 . Por lo tanto, un conjunto con n elementos tiene
. Por lo tanto, un conjunto con n elementos tiene 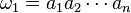 y
y 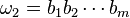 son dos palabras, la concatenación de
son dos palabras, la concatenación de 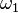 y
y 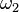 es la palabra
es la palabra