Árbol binario para niños
Un árbol binario es una forma especial de organizar información en una computadora. Imagina que tienes una serie de cajas (llamadas "nodos") y cada caja puede tener, como máximo, dos "hijos": uno a la izquierda y otro a la derecha. Por eso se llama "binario", porque "bi" significa dos.
Si una caja no tiene un hijo a la izquierda o a la derecha, decimos que esa conexión es "nula" o que no almacena ningún dato. A los nodos que no tienen hijos se les llama "nodos externos" o "hojas". Los nodos que sí tienen hijos se llaman "nodos internos".
Los árboles binarios se usan mucho en la programación para organizar datos de manera eficiente. Algunos ejemplos son los árboles binarios de búsqueda, que ayudan a encontrar información rápidamente, y los montículos binarios, que sirven para ordenar datos.
Contenido
- ¿Qué es un árbol binario en la teoría de grafos?
- Tipos de árboles binarios
- ¿Cómo se guardan los árboles binarios en la computadora?
- ¿Cómo se recorren los árboles binarios?
- Creación de árboles a partir de los recorridos
- ¿Cómo se representan los árboles generales como árboles binarios?
- Galería de imágenes
- Véase también
¿Qué es un árbol binario en la teoría de grafos?
En el mundo de las matemáticas y la computación, un árbol binario se puede ver como un dibujo de puntos y líneas donde todos los puntos están conectados, no hay caminos que formen círculos (es "acíclico"), y cada punto (o "vértice") no tiene más de dos líneas que salgan de él. Esto significa que siempre hay un solo camino para ir de un punto a otro.
Cuando elegimos un punto especial como el "origen" o "raíz" del árbol, cada punto tendrá un único "padre" (el punto del que viene) y nunca más de dos "hijos" (los puntos a los que se conecta hacia abajo).
Tipos de árboles binarios
Un árbol binario es, en esencia, una estructura donde ningún nodo puede tener más de dos ramas o "subárboles" que salgan de él. Cada nodo puede tener cero, uno o dos hijos. Al hijo de la izquierda se le llama "hijo izquierdo" y al de la derecha, "hijo derecho".
Existen diferentes tipos de árboles binarios, cada uno diseñado para tareas específicas. Algunos de los más conocidos son:
- Árbol binario de búsqueda: Muy útil para buscar y ordenar datos.
- Árbol de Fibonacci: Un tipo especial de árbol.
¿Cómo se guardan los árboles binarios en la computadora?
Las computadoras pueden guardar los árboles binarios de varias maneras. Una forma común es usando "nodos" que son como pequeñas cajas de información. Cada caja no solo guarda un dato, sino que también tiene "punteros" (como flechas) que señalan a su hijo izquierdo y a su hijo derecho. Si un nodo no tiene un hijo, su puntero simplemente apunta a "nada" (se dice que es nulo).
Otra forma de guardar un árbol binario, especialmente si es un árbol "completo" (donde todos los niveles están llenos), es usando una lista o "arreglo". En este caso, la posición de un nodo en la lista nos dice quiénes son sus hijos y su padre. Por ejemplo, si un nodo está en la posición `i`, sus hijos estarán en las posiciones `2*i + 1` y `2*i + 2`. Su padre (si tiene) estará en la posición `(i-1)/2`. Este método es muy eficiente para guardar datos y encontrarlos rápidamente.
¿Cómo se recorren los árboles binarios?
Recorrer un árbol binario significa visitar cada uno de sus nodos de una manera organizada. Hay dos tipos principales de recorridos: los "en profundidad" y los "en amplitud".
Recorridos en profundidad
Estos recorridos van lo más profundo posible por una rama antes de pasar a la siguiente.
Recorrido en preorden
En este recorrido, primero se "visita" el nodo actual (por ejemplo, se lee su valor), luego se recorre todo su subárbol izquierdo y, finalmente, se recorre todo su subárbol derecho. El orden es: nodo actual, izquierda, derecha.
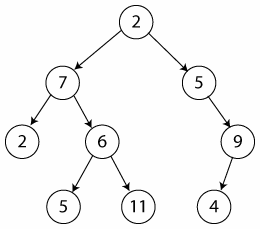
Si tuviéramos un árbol con la raíz 2, y sus hijos fueran 7 (izquierda) y 5 (derecha), y el 7 tuviera hijos 2 (izquierda) y 6 (derecha), el recorrido en preorden sería: 2, 7, 2, 6, 5, 11, 5, 9 y 4.
Recorrido en postorden
Aquí, primero se recorre todo el subárbol izquierdo, luego todo el subárbol derecho y, por último, se visita el nodo actual. El orden es: izquierda, derecha, nodo actual.
Para el mismo árbol, el recorrido en postorden sería: 2, 5, 11, 6, 7, 4, 9, 5 y 2.
Recorrido en inorden
En este recorrido, primero se visita el subárbol izquierdo, luego el nodo actual y, finalmente, el subárbol derecho. El orden es: izquierda, nodo actual, derecha.
Si el árbol es un árbol binario de búsqueda, este recorrido nos daría los valores de los nodos ordenados de menor a mayor. Para el árbol de ejemplo, el recorrido en inorden sería: 2, 7, 5, 6, 11, 2, 5, 4, 9.
Recorridos en amplitud (o por niveles)
A diferencia de los recorridos en profundidad, este método visita los nodos nivel por nivel. Primero se visita el nodo raíz (nivel 1), luego todos los nodos del nivel 2, después todos los del nivel 3, y así sucesivamente.
Para el árbol de ejemplo, el recorrido en amplitud sería: 2, 7, 5, 2, 6, 9, 5, 11 y 4.
Este tipo de recorrido no es recursivo (no se llama a sí mismo), sino que usa una "cola" (como una fila en el supermercado) para recordar qué nodos debe visitar a continuación.
Creación de árboles a partir de los recorridos
Para poder dibujar o reconstruir un árbol binario, generalmente necesitamos al menos dos de los recorridos en profundidad (preorden, inorden o postorden). Si hay nodos con valores repetidos, es mejor tener los tres recorridos para evitar confusiones.
El método consiste en usar el recorrido en preorden (el primer nodo es la raíz) o postorden (el último nodo es la raíz) para encontrar la raíz del árbol. Luego, se usa el recorrido en inorden para saber qué nodos pertenecen al subárbol izquierdo y cuáles al subárbol derecho de esa raíz. Se repite este proceso para cada subárbol hasta que todos los nodos estén ubicados.
Por ejemplo, si tenemos los recorridos:
- Preorden: 2, 7, 2, 6, 5, 11, 5, 9, 4
- Inorden: 2, 7, 5, 6, 11, 2, 5, 4, 9
- Postorden: 2, 5, 11, 6, 7, 4, 9, 5, 2
La raíz principal es el último 2 (del postorden) o el primer 2 (del preorden). Si el primer 2 fuera la raíz, no habría rama izquierda. Pero si es el 2 del medio, entonces los nodos a su izquierda en el inorden (2, 7, 5, 6, 11) forman el subárbol izquierdo, y los de su derecha (5, 4, 9) forman el subárbol derecho. Se continúa este proceso para cada subárbol hasta completar el árbol.
¿Cómo se representan los árboles generales como árboles binarios?
Es posible transformar cualquier tipo de árbol (que puede tener muchos hijos por nodo, no solo dos) en un árbol binario. Esto es muy útil en algunos lenguajes de programación.
La idea es que cada nodo del árbol original se convierte en un nodo en el árbol binario. El hijo izquierdo de este nuevo nodo binario será el primer hijo del nodo original. Y el hijo derecho será el "siguiente hermano" del nodo original (es decir, el siguiente hijo del mismo padre).
Imagina que los hijos de un nodo están conectados en una cadena. El nodo principal solo apunta al inicio de esa cadena con su puntero izquierdo, y el puntero derecho de cada hijo apunta al siguiente hijo en la cadena.
Por ejemplo, si un nodo 'A' tiene hijos 'B', 'C', 'D', 'E', 'F', 'G', en el árbol binario 'A' apuntaría a 'B' con su puntero izquierdo. Luego, 'B' apuntaría a 'C' con su puntero derecho, 'C' a 'D' con su derecho, y así sucesivamente.
Galería de imágenes
Véase también
 En inglés: Binary tree Facts for Kids
En inglés: Binary tree Facts for Kids
- Árbol (estructura de datos)
- Árbol multirrama