Orientabilidad para niños

Un toro es una superficie orientable

La Banda de Möbius es una superficie no orientable. Téngase en cuenta que el cangrejo violinista que se mueve a su alrededor ha girado hacia la izquierda y hacia la derecha con cada circulación completa. Esto no sucedería si el cangrejo estuviera en la superficie tórica

La superficie de Steiner es no orientable

En matemáticas, la orientabilidad es una propiedad de algunos espacios topológicos como el espacio vectorial, el espacio euclídeo, las superficies y, más generalmente, las variedades, que permite una definición coherente de los conceptos sentido horario y sentido antihorario. Un espacio es orientable si existe tal definición consistente. En este caso, hay dos definiciones posibles, y una elección entre ellas es una orientación del espacio. Los espacios vectoriales reales, los espacios euclídeos y las esferas son orientables. 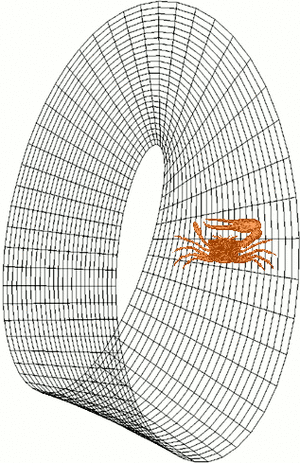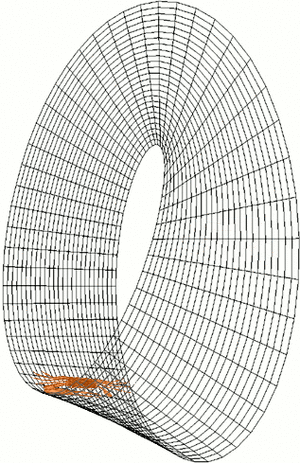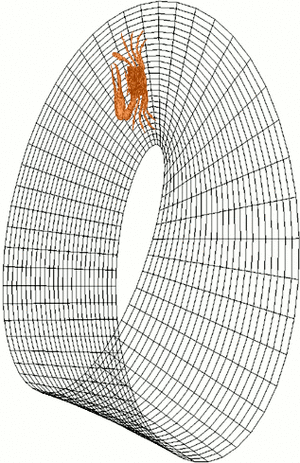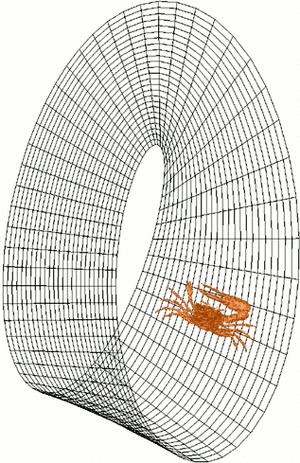Un espacio es no orientable si recorrida "en el sentido de las agujas del reloj" se cambia "al sentido contrario a las agujas del reloj" después de recorrer algunos bucles en él y volver al punto de partida. Esto significa que una forma, como , que se mueve continuamente en dicho bucle se transforma en su propia imagen especular . Una banda de Möbius es un ejemplo de un espacio no orientable.

Se pueden dar varias formulaciones equivalentes de orientabilidad, según la aplicación deseada y el nivel de generalidad. Las formulaciones aplicables a variedades topológicas generales a menudo emplean métodos de homología, mientras que para variedades diferenciables hay más estructuras presentes, lo que permite una formulación en términos de forma diferencial. Una generalización de la noción de orientabilidad de un espacio es la de orientabilidad de una familia de espacios parametrizados por algún otro espacio (un fibrado) para lo cual se debe seleccionar una orientación en cada uno de los espacios que varía continuamente con respecto a los cambios en los valores del parámetro.

Superficies orientables

En esta animación, se hace una analogía simple utilizando un engranaje que gira según la regla de la mano derecha en el vector normal de una superficie. La orientación de las curvas que marcan los límites de la superficie está dada por la dirección en la que se mueven los puntos cuando son empujados por el engranaje en movimiento. En una superficie no orientable, como la cinta de Möbius, el límite tendría que moverse en ambas direcciones a la vez, lo que no es posible

Una superficie S en un espacio euclídeo R³ es orientable si una figura bidimensional (por ejemplo, ) no se puede mover alrededor de la superficie y regresar a donde comenzó para que se vea como su propia imagen especular (). De lo contrario, la superficie es no orientable. Una superficie abstracta (es decir, una variedad bidimensional) es orientable si se puede definir un concepto consistente de rotación en el sentido de las agujas del reloj en la superficie de manera continua. Es decir, un bucle que gira en un sentido sobre la superficie nunca puede deformarse continuamente (sin superponerse a sí mismo) en un bucle que gira en el sentido opuesto. Esto resulta ser equivalente a la pregunta de si la superficie no contiene ningún subconjunto que sea un homeomorfismo a la banda de Möbius. Así, para las superficies, la banda de Möbius puede considerarse la fuente de toda falta de orientabilidad.

Para una superficie orientable, una elección consistente de "sentido horario" (en oposición a "sentido antihorario") se denomina "orientación" y la superficie se denomina "orientada". Para las superficies incrustadas en el espacio euclídeo, la orientación se especifica mediante la elección de una dirección normal n que varía continuamente en cada punto. Si tal normal existe, siempre hay dos formas de seleccionarla: n o −n. Más generalmente, una superficie orientable admite exactamente dos orientaciones, y la distinción entre una superficie "orientada" y una superficie "orientable" es sutil y frecuentemente difusa. Una superficie orientable es una superficie abstracta que admite una orientación, mientras que una superficie orientada es una superficie abstractamente orientable, y tiene el dato adicional de elegir una de las dos orientaciones posibles.

Ejemplos

La mayoría de las superficies que se encuentran en el mundo físico son orientables. Las esferas, los planos y las superficies tóricas son orientables, por ejemplo. Pero la banda de Möbius, el plano proyectivo real y la botella de Klein no son orientables. Estos últimos elementos, tal como se visualizan en 3 dimensiones, todos tienen un solo lado. El plano proyectivo real y la botella de Klein no se pueden incrustar en R³, y solo pueden someterse a inmersión mediante intersecciones.

Debe tenerse en cuenta que, localmente, una superficie sometida a inmersión siempre tiene dos lados, por lo que una hormiga miope que se desplazara sobre una superficie de un solo lado pensaría que hay "otro lado". La esencia de la unilateralidad es que la hormiga puede trasladarse de un lado de la superficie al "otro" sin atravesar la superficie o dar la vuelta sobre un borde, sino simplemente moviéndose lo suficiente.

En general, la propiedad de ser orientable no equivale a ser de dos caras; sin embargo, esto es válido cuando el espacio envolvente (como R³ en los casos anteriores) es orientable. Por ejemplo, una superficie tórica inmersa en

puede ser de un solo lado, y una botella de Klein en el mismo espacio puede ser de dos lados; aquí se refiere a la botella de Klein.

Orientación por triangulación

Cualquier superficie tiene una triangulación: una descomposición en triángulos tal que cada borde de un triángulo está pegado como máximo a otro borde. Cada triángulo se orienta eligiendo una dirección alrededor del perímetro del triángulo, asociando una dirección a cada borde del triángulo. Si esto se hace de tal manera que, cuando se pegan, los bordes vecinos apuntan en la dirección opuesta, entonces esto determina la orientación de la superficie. Tal elección solo es posible si la superficie es orientable, y en este caso hay exactamente dos orientaciones diferentes.

Si la figura se puede posicionar consistentemente en todos los puntos de la superficie sin convertirse en su imagen especular, esto inducirá una orientación en el sentido anterior en cada uno de los triángulos de la triangulación seleccionando la dirección de cada uno de los triángulos con base en en el orden rojo-verde-azul de colores de cualquiera de las figuras en el interior del triángulo.

Este enfoque se generaliza a cualquier variedad de orden n que tenga una triangulación. Sin embargo, algunas variedades de orden 4 no tienen triangulación y, en general, para n > 4, algunas variedades de n tienen triangulaciones que no son equivalentes.

Orientabilidad y homología

Si H₁(S) denota el primer grupo de homología de una superficie S, entonces S es orientable si y solo si H₁(S ) tiene un subgrupo de torsión trivial. Más precisamente, si S es orientable, entonces H₁(S) es un grupo abeliano libre, y si no, H₁(S) = F + Z/2Z donde F es abeliano libre, y se genera el factor Z/2Z por la curva central en una banda de Möbius inmersa en S.

Orientabilidad de variedades

Sea M una n-variedad topológica conexa. Hay varias definiciones posibles de lo que significa que M sea orientable. Algunas de estas definiciones requieren que M tenga una estructura adicional, como ser diferenciable. Ocasionalmente, n= 0 debe convertirse en un caso especial. Cuando se aplica más de una de estas definiciones a M, entonces M es orientable bajo una definición si y solo si es orientable bajo las otras.

Orientabilidad de variedades diferenciables

Las definiciones más intuitivas requieren que M sea una variedad diferenciable. Esto significa que las funciones de transición en el atlas de M son funciones C¹. Tal función admite un determinante jacobiano. Cuando el determinante jacobiano es positivo, se dice que la función de transición conserva la orientación. Un atlas orientado en M es un atlas para el cual todas las funciones de transición conservan la orientación. M es orientable si admite un atlas orientado. Cuando n > 0, una orientación de M es un atlas orientado al máximo (de forma que n= 0, una orientación de M, es una función M → {±1}).

La orientabilidad y las orientaciones también se pueden expresar en términos del haz de tangentes. El haz de tangentes es un fibrado vectorial, por lo que posee una estructura de grupo GL(n, R). Es decir, las funciones de transición de la variedad inducen funciones de transición en el haz tangente que son transformaciones lineales por fibrado. Si el grupo de estructuras se puede reducir al grupo GL⁺(n, R) de matrices determinantes positivas, o de manera equivalente si existe un atlas cuyas funciones de transición determinan una orientación que preserva la transformación lineal en cada espacio tangente, entonces la variedad M es orientable. Por el contrario, M es orientable si y solo si el grupo de estructuras del haz tangente se puede reducir de esta manera. Se pueden hacer observaciones similares para el haz de marcos.

Otra forma de definir orientaciones en una variedad diferenciable es a través de su forma de volumen. Una forma de volumen es una sección omega que no desaparece en parte alguna de ⋀ⁿ T^* M, la potencia exterior superior del haz cotangente de M. Por ejemplo, Rⁿ tiene una forma de volumen estándar dada por dx¹ ∧ ⋯ ∧ dxⁿ. Dada una forma de volumen en M, la colección de todos los gráficos U → Rⁿ para los que la forma de volumen estándar retrocede a un múltiplo positivo de omega; es un atlas orientado. La existencia de una forma de volumen es, por lo tanto, equivalente a la orientabilidad de la variedad.

Las formas de volumen y los vectores tangentes se pueden combinar para dar otra descripción de la orientabilidad. Si X₁, …, X_n es una base de vectores tangentes en un punto p, entonces se dice que la base es destrógira si ω(X₁, …, X_n) > 0. Una función de transición conserva la orientación si y solo si envía bases destrógiras a bases destrógiras. La existencia de una forma de volumen implica una reducción del grupo estructural del haz tangente o del haz de marcos a GL⁺(n, R). Como antes, esto implica la orientabilidad de M. Por el contrario, si M es orientable, entonces las formas de volumen local pueden unirse para crear una forma de volumen global, siendo necesaria la orientabilidad para garantizar que la forma global no desaparezca.

La homología y la orientabilidad de las variedades generales

En el corazón de todas las definiciones anteriores de orientabilidad de una variedad diferenciable está la noción de una función de transición que preserva la orientación. Esto plantea la cuestión de qué preservan exactamente tales funciones de transición. No pueden preservar una orientación de la variedad porque una orientación de la variedad es un atlas, y no tiene sentido decir que una función de transición conserva o no conserva un atlas del cual es miembro.

Esta cuestión se puede resolver definiendo orientaciones locales. En una variedad unidimensional, una orientación local alrededor de un punto p corresponde a la elección del sentido a la izquierda o a la derecha cerca de ese punto. En una variedad bidimensional, corresponde a una elección de sentido horario y antihorario. Estas dos situaciones comparten la característica común de que se describen en términos de comportamiento de dimensión superior cerca de p pero no en p. Para el caso general, sea M una variedad topológica n. Una orientación local de M alrededor de un punto p es una elección de generador del grupo

Para ver el significado geométrico de este grupo, elíjase un gráfico alrededor de p. En ese gráfico hay una vecindad de p que es una bola abierta B alrededor del origen O. Por el teorema de escisión, es isomorfo a . La bola B es contráctil, por lo que sus grupos de homología desaparecen excepto en el grado cero, y el espacio B \ O es una esfera (n − 1), por lo que sus grupos de homología desaparecen excepto en los grados n − 1 y 0. Un cálculo con sucesión exacta mediante una homología relativa muestra que el grupo de homología anterior es isomorfo a . Por lo tanto, la elección del generador corresponde a la decisión de si, en el grafo dado, una esfera alrededor de p es positiva o negativa. Un reflejo de Rⁿ a través del origen actúa por negación sobre , por lo que el significado geométrico de la elección del generador es que distingue los grafos de sus imágenes reflejadas.

En una variedad topológica, una función de transición conserva la orientación si, en cada punto p de su dominio, fija los generadores de . A partir de aquí, las definiciones relevantes son las mismas que en el caso diferenciable. Un atlas orientado es aquel para el que todas las funciones de transición conservan la orientación, M es orientable si admite un atlas orientado, y cuando n > 0, una orientación de M es un atlas orientado al máximo.

Intuitivamente, una orientación de M debería definir una única orientación local de M en cada punto. Esto se precisa al notar que cualquier gráfico en el atlas orientado alrededor de p puede usarse para determinar una esfera alrededor de p, y esta esfera determina un generador de . Además, cualquier otro gráfico alrededor de p está relacionado con el primer gráfico mediante una función de transición que preserva la orientación, y esto implica que los dos gráficos producen el mismo generador, por lo que el generador es único.

También son posibles definiciones puramente homológicas. Asumiendo que M es cerrado y conexo, M es orientable si y solo si el n grupo de homología es isomorfo a los enteros Z. Una orientación de M es una elección del generador α de este grupo. Este generador determina una carta orientada fijando un generador del grupo cíclico infinito y tomando las cartas orientadas como aquellas para las que α avanza hacia el generador fijo. Por el contrario, un atlas orientado determina un generador de este tipo, ya que las orientaciones locales compatibles se pueden unir para dar un generador para el grupo de homología .

Orientación y cohomología

Una variedad M es orientable si y solo si la primera clase de Stiefel-Whitney desaparece. En particular, si el primer grupo de cohomología con coeficientes Z/2 es cero, entonces la variedad es orientable. Además, si M es orientable y w₁ desaparece, entonces parametriza las opciones de orientación. Esta caracterización de la orientabilidad se extiende a la orientabilidad de haces vectoriales generales sobre M, no solo al haz tangente.

La cubierta doble de orientación

Alrededor de cada punto de M hay dos orientaciones locales. Intuitivamente, existe una forma de pasar de una orientación local en un punto p a una orientación local en un punto cercano p′: cuando los dos puntos se encuentran en el mismo gráfico de coordenadas U → Rⁿ, ese gráfico de coordenadas define orientaciones locales compatibles en p y p′. Por lo tanto, al conjunto de orientaciones locales se le puede dar una topología, y esta topología lo convierte en una variedad.

Más precisamente, sea O el conjunto de todas las orientaciones locales de M. Para topologizar O se especifica una subbase para establecer su topología. Sea U un subconjunto abierto de M elegido de manera que sea isomorfo a Z. Supóngase que α es un generador de este grupo. Para cada p en U, existe una función que avanza de manera que . El codominio de este grupo tiene dos generadores, y α se aplica sobre uno de ellos. La topología en O se define de modo que

es abierto.

Existe una aplicación canónica π : O → M que envía una orientación local en p a p. Está claro que cada punto de M tiene precisamente dos preimágenes bajo π. De hecho, π es incluso un homeomorfismo local, porque las preimágenes de los conjuntos abiertos U mencionados anteriormente son homeomorfas a la unión disjunta de dos copias de U. Si M es orientable, entonces M en sí mismo es uno de estos conjuntos abiertos, por lo que O es la unión disjunta de dos copias de M. Sin embargo, si M no es orientable, entonces O es conexo y orientable. El colector O se denomina doble recubrimiento de orientación.

Variedades con borde

Si M es una variedad con borde, entonces una orientación de M se define como una orientación de su interior. Una orientación de M induce una orientación del borde ∂M: sea una carta de M que, cuando se restringe al interior, produce la orientación . La restricción de esta carta a ∂M es una carta de ∂M. El conjunto de todas las cartas que se pueden construir así forma un atlas orientado para ∂M.

Cuando M es suave, en cada punto p de ∂M, la restricción del fibrado tangente de M a ∂M es isomorfa a T_p∂M ⊕ R, donde el factor de R se describe mediante el vector normal que apunta hacia adentro. La orientación canónica de T_p∂M está definida por la condición de que una base de T_p∂M esté orientada positivamente si y solo si cuando se precede por el vector normal exterior define una base orientada positivamente de T_pM.

Doble recubrimiento orientable

Una noción estrechamente relacionada utiliza la idea de espacio recubridor. Para una variedad conexa M, tómese M^∗, el conjunto de pares (x, o) donde x es un punto de M y o es una orientación en x. Aquí se asume que M es suave, por lo que se puede elegir una orientación en el espacio tangente en un punto o usarse una homología singular para definir la orientación. Luego, para cada subconjunto abierto y orientado de M, se considera el conjunto de pares correspondiente y se define como un conjunto abierto de M^∗. Esto le da a M^∗ una topología y el envío de proyección (x, o) a x es entonces una aplicación de recubrimiento de 2 a 1. Este espacio de cobertura se denomina doble cobertura orientable, ya que es orientable. M^∗ es conexo si y solo si M no es orientable.

Otra forma de construir este recubrimiento es dividir los bucles basados ​​en un punto base en bucles que conservan la orientación o que invierten la orientación. Los bucles que conservan la orientación generan un subgrupo del grupo fundamental que es el grupo completo o de índice dos. En el último caso (lo que significa que hay un camino de inversión de la orientación), el subgrupo corresponde a un doble recubrimiento conexo, que es orientable por construcción. En el primer caso, se puede simplemente tomar dos copias de M, cada una de las cuales corresponde a una orientación diferente.

Orientación de haces vectoriales

Un fibrado vectorial real, que a priori tiene una estructura de grupo GL(n), se denomina orientable cuando el fibrado puede ser reducido a , el grupo de matrices con determinante positivo. Para el fibrado tangente, esta reducción siempre es posible si la variedad base subyacente es orientable y, de hecho, esto proporciona una manera conveniente de definir la orientabilidad de una variedad real suave: se define que una variedad suave es orientable si su fibrado tangente es orientable (como un haz de vectores). Téngase en cuenta que, como variedad por derecho propio, el haz tangente es siempre orientable, incluso sobre variedades no orientables.

Conceptos relacionados

Geometría lorentziana

En geometría lorentziana, hay dos tipos de orientabilidad: la orientabilidad espacial y la orientabilidad temporal. Estos conceptos juegan un importante papel en la estructura causal del espacio-tiempo. En el contexto de la relatividad general, una variedad espacio-tiempo es orientable en el espacio si, cada vez que dos observadores diestros inician un recorrido en naves espaciales partiendo del mismo punto del espacio-tiempo y luego se encuentran de nuevo en otro punto, siguen siendo diestros uno con respecto al otro. Si un espacio-tiempo es orientable en el tiempo, entonces los dos observadores siempre estarán de acuerdo en la dirección del tiempo en ambos puntos de su encuentro. De hecho, un espacio-tiempo es orientable en el tiempo si y solo si dos observadores cualesquiera pueden ponerse de acuerdo sobre cuál de los dos encuentros precedió al otro.

Formalmente, el grupo pseudo-ortogonal O(p,q) tiene un par de caracteres: el carácter de orientación espacial σ₊ y el carácter de orientación temporal σ₋,

Su producto sigma; = σ₊σ₋ es el determinante, que da el carácter de orientación. Una orientación espacial de una variedad pseudo-riemanniana se identifica con una sección del fibrado asociado

donde O(M) es el paquete de marcos pseudo-ortogonales. De manera similar, una orientación temporal es una sección del haz asociado

Véase también

En inglés: Orientability Facts for Kids

• Orientación de una curva
• Haz de orientación