Sistema binario para niños
El sistema binario es una forma de contar y representar números usando solo dos símbolos: el 0 (cero) y el 1 (uno). También se le llama sistema diádico en el mundo de la computación.
Este sistema es muy importante porque las computadoras lo usan para funcionar. Internamente, las computadoras trabajan con dos estados eléctricos: "apagado" (que representa el 0) y "encendido" (que representa el 1). Por eso, el sistema binario es su lenguaje natural.
Contenido
- Historia del sistema binario
- Representación de números binarios
- Conversión entre binario y decimal
- Operaciones con números binarios
- Conversión entre sistema binario y octal
- Conversión entre binario y hexadecimal
- Tabla de conversión de sistemas numéricos
- Galería de imágenes
- Véase también
Historia del sistema binario
El sistema binario que usamos hoy fue estudiado en Europa en los siglos XVI y XVII por personas como Thomas Harriot, Juan Caramuel Lobkowitz y Gottfried Leibniz. Pero, ¡sabías que ideas similares al sistema binario ya existían mucho antes en otras culturas?
Orígenes antiguos del sistema binario
El concepto de usar solo dos estados para representar información no es nuevo.
En el antiguo Egipto
Los antiguos egipcios tenían un sistema para sus fracciones llamado "fracciones del Ojo de Horus". Este sistema usaba fracciones como 1/2, 1/4, 1/8, y así sucesivamente, que son potencias de dos. Esto les permitía medir cantidades de granos o líquidos. Las primeras ideas de este sistema se ven en documentos de hace unos 4400 años.
En China
En la antigua China, un libro muy famoso llamado el I Ching describe una serie de símbolos que son como números binarios. Estos símbolos, llamados trigramas y hexagramas, representan combinaciones de líneas continuas y partidas, que son como el 0 y el 1. Un filósofo chino llamado Shao Yong, en el siglo XI, incluso organizó estos hexagramas de una manera que se parece a cómo ordenamos los números binarios del 0 al 63.
En la India
Un antiguo matemático indio, Acharya Pingala, creó un sistema binario para describir la poesía. Usaba sílabas cortas y largas, que eran como los dos símbolos del sistema binario. Esto es un poco parecido al código Morse.
Otras culturas con ideas binarias
Incluso en la isla de Mangareva, en la Polinesia Francesa, se usaba un sistema que mezclaba el binario y el decimal antes del año 1450. También se han encontrado ideas binarias en sistemas de adivinación de África y en la geomancia medieval de Occidente.
Pioneros occidentales del sistema binario
Antes de Leibniz, otros pensadores exploraron ideas binarias.
Francis Bacon y la codificación
En 1605, Francis Bacon imaginó un sistema para convertir las letras del alfabeto en secuencias de dígitos binarios. Estas secuencias podrían esconderse en textos normales, cambiando muy poco la forma de las letras.
Juan Caramuel y su libro
En 1670, Juan Caramuel publicó un libro donde explicaba el sistema binario en algunas de sus páginas.
Leibniz y el sistema binario moderno
Gottfried Leibniz fue quien documentó completamente el sistema binario moderno en el siglo XVIII. En su escrito "Explication de l'Arithmétique Binaire", mencionó los símbolos binarios chinos. Leibniz vio cómo un sistema con solo dos variables (0 y 1) podía usarse para organizar información, de forma similar a como funciona el sistema binario actual.
Avances importantes después de Leibniz
El Álgebra de Boole
En 1854, el matemático británico George Boole publicó un trabajo muy importante. Creó un sistema de lógica que hoy conocemos como Álgebra de Boole. Este sistema fue clave para desarrollar el sistema binario que usamos en la electrónica y las computadoras.
Circuitos digitales y computadoras
En 1937, Claude Shannon hizo su tesis doctoral en el MIT. En ella, mostró cómo usar el Álgebra de Boole y la aritmética binaria con relés (interruptores eléctricos) y conmutadores. Su tesis, "Un Análisis Simbólico de Circuitos Conmutadores y Relés", sentó las bases para el diseño de los circuitos digitales que están en todos nuestros aparatos electrónicos.
En noviembre de 1937, George Robert Stibitz, de los Laboratorios Bell, construyó una calculadora llamada "Modelo K". Esta calculadora usaba la suma binaria para hacer sus cálculos. En 1940, los Laboratorios Bell crearon una "Calculadora de Números Complejos" que podía hacer cálculos más avanzados. Lo más sorprendente fue que, en una demostración, Stibitz pudo controlar esta calculadora a distancia usando una línea telefónica. ¡Fue la primera vez que una computadora se usó de forma remota!
Representación de números binarios
En el sistema binario, solo necesitamos el 0 y el 1. Una secuencia de estos dígitos se llama "bits" (dígitos binarios). En una computadora, estos bits pueden representar dos voltajes diferentes o polaridades magnéticas en un disco.
Los números binarios se escriben a menudo con un pequeño número 2 abajo (subíndice) o con prefijos/sufijos para indicar que son binarios. Por ejemplo, todas estas formas significan lo mismo:
- 100101 binario
- 100101b
- 100101B
- bin 100101
- 1001012
- %100101
- 0b100101 (común en lenguajes de programación)
Conversión entre binario y decimal
Es útil saber cómo pasar números de nuestro sistema decimal (base 10) al binario (base 2) y viceversa.
Decimal a binario
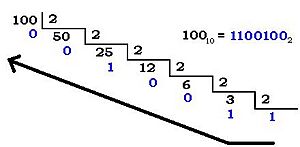
Para convertir un número decimal a binario, lo dividimos entre 2 una y otra vez.
Método de divisiones sucesivas
1. Divide el número decimal entre 2. 2. Anota el residuo (lo que sobra: 0 o 1). 3. Toma el resultado de la división (el cociente) y vuelve a dividirlo entre 2. 4. Repite hasta que el cociente sea 0 o 1. 5. El número binario se forma leyendo los residuos de abajo hacia arriba, empezando por el último cociente.
- Ejemplo
- Convertir el número decimal 131 a binario.
- 131 ÷ 2 = 65, residuo 1
- 65 ÷ 2 = 32, residuo 1
- 32 ÷ 2 = 16, residuo 0
- 16 ÷ 2 = 8, residuo 0
- 8 ÷ 2 = 4, residuo 0
- 4 ÷ 2 = 2, residuo 0
- 2 ÷ 2 = 1, residuo 0
- Último cociente es 1.
Ahora, leemos los residuos y el último cociente de abajo hacia arriba: 10000011. Así, 131 en decimal es 10000011 en binario.
Decimal con decimales a binario
Si tienes un número decimal con una parte fraccionaria (como 5.5), lo conviertes así: 1. Convierte la parte entera a binario (como en el ejemplo anterior). 2. Para la parte decimal, multiplica la parte decimal por 2. 3. Si el resultado es 1 o más, anota un 1 y sigue multiplicando solo la parte decimal del resultado. 4. Si el resultado es menor que 1, anota un 0 y sigue multiplicando el resultado. 5. Repite hasta que la parte decimal sea 0 o hasta que tengas suficientes dígitos. 6. Coloca los dígitos binarios de la parte decimal después de la coma.
- Ejemplo
- Convertir 0.3125 (decimal) a binario.
- 0.3125 × 2 = 0.625 → 0
- 0.625 × 2 = 1.25 → 1 (tomamos solo 0.25 para la siguiente)
- 0.25 × 2 = 0.5 → 0
- 0.5 × 2 = 1.0 → 1 (la parte decimal es 0, terminamos)
Los dígitos binarios son 0101. Así, 0.3125 en decimal es 0.0101 en binario.
Binario a decimal
Para convertir un número binario a decimal, sumamos las potencias de 2.
Método de potencias de 2
1. Empieza por el dígito más a la derecha del número binario. 2. Multiplica cada dígito por 2 elevado a una potencia, empezando por 20 (que es 1) para el dígito más a la derecha, luego 21 (que es 2), 22 (que es 4), y así sucesivamente, aumentando la potencia en 1 por cada posición hacia la izquierda. 3. Suma todos los resultados.
- Ejemplo
- Convertir 1010010 (binario) a decimal.
- 0 × 20 = 0 × 1 = 0
- 1 × 21 = 1 × 2 = 2
- 0 × 22 = 0 × 4 = 0
- 0 × 23 = 0 × 8 = 0
- 1 × 24 = 1 × 16 = 16
- 0 × 25 = 0 × 32 = 0
- 1 × 26 = 1 × 64 = 64
Suma los resultados: 0 + 2 + 0 + 0 + 16 + 0 + 64 = 82. Así, 1010010 en binario es 82 en decimal.
Binario con decimales a decimal
Si el número binario tiene una parte decimal (como 101.1), la parte entera se convierte igual. Para la parte decimal: 1. Empieza por el primer dígito a la derecha de la coma. 2. Multiplica cada dígito por 2 elevado a una potencia negativa, empezando por 2-1 (que es 0.5), luego 2-2 (que es 0.25), y así sucesivamente. 3. Suma todos los resultados.
- Ejemplo
- Convertir 101.1 (binario) a decimal.
- Parte entera (101):
- 1 × 20 = 1
- 0 × 21 = 0
- 1 × 22 = 4
- Suma: 1 + 0 + 4 = 5
- Parte decimal (.1):
- 1 × 2-1 = 1 × 0.5 = 0.5
Suma ambas partes: 5 + 0.5 = 5.5. Así, 101.1 en binario es 5.5 en decimal.
Operaciones con números binarios
Podemos sumar, restar, multiplicar y dividir números binarios, igual que con los números decimales.
Suma de números binarios
Las reglas básicas de la suma binaria son:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (esto significa 0 y "llevamos" 1 a la siguiente columna, como cuando sumamos 9 + 1 = 10 en decimal)
- Ejemplo
- Sumar 10011000 + 00010101
``` 10011000 + 00010101
10101101 ``` Empezamos por la derecha:
- 0 + 1 = 1
- 0 + 0 = 0
- 1 + 1 = 10 (escribimos 0, llevamos 1)
- 1 (que llevamos) + 1 + 0 = 10 (escribimos 0, llevamos 1)
- 1 (que llevamos) + 0 + 1 = 10 (escribimos 0, llevamos 1)
- 1 (que llevamos) + 0 + 0 = 1
- 0 + 0 = 0
- 1 + 0 = 1
El resultado es 10101101.
Resta de números binarios
Las reglas básicas de la resta binaria son:
- 0 - 0 = 0
- 1 - 0 = 1
- 1 - 1 = 0
- 0 - 1 = 1 (y "pedimos prestado" 1 de la siguiente columna, como cuando restamos en decimal)
- Ejemplo
- Restar 10001 - 01010
``` 10001 - 01010
00111 ``` Empezamos por la derecha:
- 1 - 0 = 1
- 0 - 1: No se puede. Pedimos prestado al siguiente 0, que a su vez pide prestado al siguiente 0, y así hasta el 1. El 1 se convierte en 0, el primer 0 en 10 (que es 2 en decimal), el siguiente 0 en 1, y el último 0 en 10 (2 en decimal).
- Entonces, 10 - 1 = 1 (en la segunda posición desde la derecha).
- En la tercera posición, teníamos un 0 que se convirtió en 1 (por el préstamo), y restamos 0: 1 - 0 = 1.
- En la cuarta posición, teníamos un 0 que se convirtió en 1, y restamos 1: 1 - 1 = 0.
- En la quinta posición, teníamos un 1 que se convirtió en 0, y restamos 0: 0 - 0 = 0.
El resultado es 00111.
Multiplicación de números binarios
Las reglas básicas de la multiplicación binaria son:
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1
El proceso es igual que en decimal: multiplicamos por cada dígito del segundo número y luego sumamos los resultados.
- Ejemplo
- Multiplicar 10110 × 1001
``` 10110 x 1001
10110 (10110 × 1) 00000 (10110 × 0, desplazado) 00000 (10110 × 0, desplazado) 10110 (10110 × 1, desplazado)
11000110 ``` El resultado es 11000110.
División de números binarios
La división binaria es similar a la decimal. La única diferencia es que las restas dentro de la división deben hacerse en binario.
- Ejemplo
- Dividir 100010010 (274 en decimal) entre 1101 (13 en decimal)
``` 100010010 / 1101 = 010101 -0000 ------- 10001 -1101 ------- 01000 - 0000 ------- 10000 - 1101 ------- 00111 - 0000 ------- 01110 - 1101 ------- 00001 ``` El cociente es 010101 (que es 21 en decimal) y el residuo es 00001 (que es 1 en decimal).
Conversión entre sistema binario y octal
El sistema octal usa 8 dígitos (0-7). Como 8 es 2 elevado a la potencia 3 (23), podemos convertir fácilmente entre binario y octal agrupando los bits.
Binario a octal
1. Agrupa los dígitos binarios de 3 en 3, empezando desde la derecha. Si al final te faltan dígitos, añade ceros a la izquierda. 2. Convierte cada grupo de 3 bits a su dígito octal equivalente usando la tabla. 3. Junta los dígitos octales de izquierda a derecha.
| Número en binario | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Número en octal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
- Ejemplo
- Convertir 11001111 (binario) a octal.
- Agrupamos de 3 en 3 desde la derecha: 11 | 001 | 111
- Añadimos ceros a la izquierda para completar el primer grupo: 011 | 001 | 111
- Convertimos cada grupo:
- 011 = 3
- 001 = 1
- 111 = 7
- Juntamos los resultados: 317.
Así, 11001111 en binario es 317 en octal.
Octal a binario
Cada dígito octal se convierte en su equivalente binario de 3 bits.
- Ejemplo
- Convertir 247 (octal) a binario.
- 2 en octal es 010 en binario (de 3 bits).
- 4 en octal es 100 en binario.
- 7 en octal es 111 en binario.
- Juntamos los bits: 010100111.
Así, 247 en octal es 010100111 en binario.
Conversión entre binario y hexadecimal
El sistema hexadecimal usa 16 dígitos (0-9 y A-F). Como 16 es 2 elevado a la potencia 4 (24), podemos convertir fácilmente entre binario y hexadecimal agrupando los bits de 4 en 4.
Binario a hexadecimal
1. Agrupa los dígitos binarios de 4 en 4, empezando desde la derecha. Si al final te faltan dígitos, añade ceros a la izquierda. 2. Convierte cada grupo de 4 bits a su dígito hexadecimal equivalente usando la tabla. 3. Junta los dígitos hexadecimales de izquierda a derecha.
| Número en binario | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Número en hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
- Ejemplo
- Convertir 110111010 (binario) a hexadecimal.
- Agrupamos de 4 en 4 desde la derecha: 1 | 1011 | 1010
- Añadimos ceros a la izquierda para completar el primer grupo: 0001 | 1011 | 1010
- Convertimos cada grupo:
- 0001 = 1
- 1011 = B
- 1010 = A
- Juntamos los resultados: 1BA.
Así, 110111010 en binario es 1BA en hexadecimal.
Hexadecimal a binario
Cada dígito hexadecimal se convierte en su equivalente binario de 4 bits.
- Ejemplo
- Convertir 6F5 (hexadecimal) a binario.
- 6 en hexadecimal es 0110 en binario (de 4 bits).
- F en hexadecimal es 1111 en binario.
- 5 en hexadecimal es 0101 en binario.
- Juntamos los bits: 011011110101.
Así, 6F5 en hexadecimal es 011011110101 en binario.
Tabla de conversión de sistemas numéricos
Esta tabla te ayuda a ver cómo se representan los mismos números en diferentes sistemas:
| Decimal | Binario | Hexadecimal | Octal | BCD | Exceso 3 | Gray o Reflejado |
|---|---|---|---|---|---|---|
| 0 | 0000 | 0 | 0 | 0000 | 0011 | 0000 |
| 1 | 0001 | 1 | 1 | 0001 | 0100 | 0001 |
| 2 | 0010 | 2 | 2 | 0010 | 0101 | 0011 |
| 3 | 0011 | 3 | 3 | 0011 | 0110 | 0010 |
| 4 | 0100 | 4 | 4 | 0100 | 0111 | 0110 |
| 5 | 0101 | 5 | 5 | 0101 | 1000 | 0111 |
| 6 | 0110 | 6 | 6 | 0110 | 1001 | 0101 |
| 7 | 0111 | 7 | 7 | 0111 | 1010 | 0100 |
| 8 | 1000 | 8 | 10 | 1000 | 1011 | 1100 |
| 9 | 1001 | 9 | 11 | 1001 | 1100 | 1101 |
| 10 | 1010 | A | 12 | 0001 0000 | 1111 | |
| 11 | 1011 | B | 13 | 0001 0001 | 1110 | |
| 12 | 1100 | C | 14 | 0001 0010 | 1010 | |
| 13 | 1101 | D | 15 | 0001 0011 | 1011 | |
| 14 | 1110 | E | 16 | 0001 0100 | 1001 | |
| 15 | 1111 | F | 17 | 0001 0101 | 1000 |
Galería de imágenes
Véase también
 En inglés: Binary number Facts for Kids
En inglés: Binary number Facts for Kids