Número irracional para niños
En matemáticas, un número irracional es un tipo de número que no se puede escribir como una fracción simple, es decir, como una división de dos números enteros (por ejemplo, 1/2 o 3/4). Su forma decimal es infinita y no tiene un patrón que se repita.
Imagina que intentas escribir un número como 2,64575131106459059050161... con infinitas cifras que nunca se repiten. Ese es un número irracional. Algunos ejemplos famosos de números irracionales son el número pi (π), el número e y el número áureo (φ).
Contenido
Números Irracionales: ¿Qué Son?
Los números irracionales son parte de los números reales. Se les llama "irracionales" porque no se pueden expresar como una "razón" o "cociente" de dos números enteros. Esto significa que no puedes encontrar dos números enteros, uno arriba y otro abajo, que al dividirlos te den exactamente ese número.
Descubriendo los Números Irracionales
La idea de los números irracionales no es nueva; se remonta a la Antigua Grecia.
¿Cómo se descubrieron?
Se cree que el descubrimiento de los números irracionales fue hecho por un matemático griego llamado Hípaso de Metaponto, que era parte de un grupo conocido como los Pitagóricos, en el siglo V a. C.. Los Pitagóricos creían que todo en el universo podía explicarse con números enteros y sus proporciones.
Hípaso descubrió un problema al estudiar la hipotenusa (el lado más largo) de un triángulo rectángulo isósceles (un triángulo con dos lados iguales y un ángulo recto). Se dio cuenta de que la longitud de la hipotenusa no podía medirse exactamente con la misma unidad que los otros lados, sin importar cuán pequeña fuera esa unidad.
Para entenderlo mejor, piensa en un cuadrado. Si los lados miden 1 unidad, la diagonal (la línea que cruza el cuadrado de una esquina a la otra) mide la raíz cuadrada de 2 (aproximadamente 1.4142135...). Hípaso demostró que este número no podía escribirse como una fracción. Esto fue un gran problema para los Pitagóricos, porque contradecía su creencia de que todo se podía expresar con números enteros.
La leyenda dice que Hípaso fue castigado por revelar este descubrimiento, ya que desafiaba las ideas matemáticas de su tiempo. Este hallazgo mostró que la geometría y los números no siempre estaban tan conectados como pensaban.
La contribución de Eudoxo
Más tarde, otro matemático griego llamado Eudoxo de Cnido desarrolló una nueva forma de entender las proporciones. Él hizo una distinción importante entre "magnitud" (como la longitud de una línea o el área de una figura, que pueden dividirse infinitamente) y "número" (que se consideraba hecho de unidades discretas). Esta idea ayudó a los matemáticos griegos a trabajar con estas cantidades "inconmensurables" (que no se pueden medir con una unidad común) sin tener que expresarlas como números enteros.
¿Cómo se representan los números irracionales?
No hay un símbolo único y universalmente aceptado para los números irracionales. A veces se usa la letra I o 
. Sin embargo, es más común definirlos como todos los números reales que no son racionales. Esto se escribe así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{I}:=\R \backslash\mathbb{Q} , que significa "los números irracionales son los números reales menos los números racionales".
Tipos de Números Irracionales
Los números irracionales se pueden clasificar en dos grupos principales:
Números Algebraicos Irracionales
Estos son números irracionales que pueden ser la solución de una ecuación algebraica simple. Una ecuación algebraica es una ecuación donde tienes variables (como 'x') elevadas a potencias y sumadas o restadas, igualadas a cero. Por ejemplo, la raíz cuadrada de 2 es un número irracional algebraico porque es la solución de la ecuación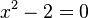 
. El número áureo (φ) también es un número irracional algebraico.
Números Trascendentes
Estos son números irracionales que no pueden ser la solución de ninguna ecuación algebraica con coeficientes (los números que acompañan a las variables) racionales. Son más "especiales" y no se pueden "atrapar" con una ecuación simple. Los ejemplos más famosos de números trascendentes son el número pi (π) y el número e.
Los números trascendentes suelen aparecer en funciones matemáticas más complejas, como las trigonométricas o las exponenciales.
Características de los Números Irracionales
- Decimales infinitos y no repetitivos: Su característica más importante es que, cuando los escribes en forma decimal, tienen infinitas cifras después del punto, y estas cifras nunca forman un patrón que se repita.
- Densidad: Entre dos números racionales diferentes, siempre hay al menos un número irracional. Esto significa que los números irracionales están "mezclados" por toda la recta numérica, llenando los "huecos" que dejan los números racionales.
- Operaciones:
* Si sumas o restas un número racional y un número irracional, el resultado siempre será un número irracional. * Si multiplicas un número racional (que no sea cero) por un número irracional, el resultado también será un número irracional. * La raíz cuadrada de cualquier número natural que no sea un cuadrado perfecto (como 4, 9, 16) es un número irracional. Por ejemplo, la raíz cuadrada de 3 es irracional.
Ejemplos de Números Irracionales
Aquí tienes algunos ejemplos de números irracionales conocidos:
- El número pi (π): Aproximadamente 3.14159... Es la relación entre la circunferencia de un círculo y su diámetro.
- El número e: Aproximadamente 2.71828... Es una constante muy importante en matemáticas, especialmente en el cálculo y el crecimiento exponencial.
- El número áureo (φ): Aproximadamente 1.61803... Aparece en la naturaleza, el arte y la arquitectura, y se considera que representa una proporción estéticamente agradable.
- La raíz cuadrada de 2: Aproximadamente 1.41421... Es la longitud de la diagonal de un cuadrado con lados de 1 unidad.
Otros ejemplos interesantes
- La Constante de Champernowne (C10): 0.12345678910111213... Se forma escribiendo todos los números enteros seguidos.
- La Constante de Copeland-Erdős (κ): 0.23571113171923... Se forma escribiendo todos los números primos seguidos.
Galería de imágenes
-
La constante matemática π, expresada en su forma decimal.
-
Diez mil primeras cifras decimales del número
.
Véase también
En inglés: Irrational number Facts for Kids
