Leyes de De Morgan para niños
Las leyes de De Morgan son reglas importantes en la lógica y en el álgebra de Boole. Estas leyes nos ayudan a cambiar cómo expresamos ideas que usan las palabras "NO", "Y" y "O". Fueron nombradas en honor a Augustus De Morgan, un matemático y lógico.
Imagina que tienes dos ideas o afirmaciones, que llamaremos P y Q. Las leyes de De Morgan nos dicen que:
- Si dices "NO (P Y Q)", es lo mismo que decir "(NO P) O (NO Q)".
* Por ejemplo, si es falso que "está lloviendo Y hace frío", entonces debe ser que "NO está lloviendo O NO hace frío".
- Si dices "NO (P O Q)", es lo mismo que decir "(NO P) Y (NO Q)".
* Por ejemplo, si es falso que "estoy leyendo O estoy jugando", entonces debe ser que "NO estoy leyendo Y NO estoy jugando".
Estas reglas son muy útiles para simplificar expresiones lógicas en la programación de computadoras y en el diseño de circuitos digitales. Son un ejemplo de un concepto más amplio llamado dualidad matemática, donde las operaciones se "intercambian" bajo ciertas condiciones.
Contenido
¿Quién fue Augustus De Morgan?
Augustus De Morgan (1806-1871) fue un matemático y lógico británico. Él presentó una versión formal de estas leyes para la lógica proposicional. Aunque la idea ya había sido observada por pensadores antiguos como Aristóteles y lógicos medievales, De Morgan fue quien las formuló de manera clara y las incorporó al lenguaje de la lógica moderna.
¿Cómo se usan las leyes de De Morgan?
Las leyes de De Morgan se pueden aplicar para simplificar expresiones lógicas complejas. Esto es muy útil en campos como la ingeniería electrónica y la informática.
En la lógica de computadoras
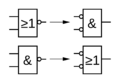
En el diseño de circuitos digitales, las leyes de De Morgan permiten a los ingenieros cambiar un tipo de puerta lógica por otro. Por ejemplo, una puerta que hace "NO Y" (NAND) puede ser reemplazada por una combinación de puertas que hacen "NO O" (NOR) y viceversa. Esto ayuda a optimizar los circuitos.
Los programadores también usan estas leyes para hacer que las sentencias condicionales (como las que usan "si... entonces...") sean más sencillas de entender o de negar. Por ejemplo, si necesitas saber cuándo una condición NO se cumple, puedes aplicar las leyes de De Morgan para reescribir esa negación de una forma más clara.
En la teoría de conjuntos
Las leyes de De Morgan también se aplican en la teoría de conjuntos, que es una rama de las matemáticas que estudia colecciones de objetos. Aquí, las leyes se refieren a cómo la negación (o el "complemento") afecta a la unión de conjuntos (que es como el "O") y a la intersección de conjuntos (que es como el "Y").
Se pueden expresar así:
- El complemento de la unión de dos conjuntos es igual a la intersección de sus complementos.
- El complemento de la intersección de dos conjuntos es igual a la unión de sus complementos.
Una forma sencilla de recordar esto es la regla "romper la línea, cambiar el signo". Si tienes una línea sobre una expresión (que significa "NO" o "complemento"), puedes "romper" esa línea sobre los elementos individuales, pero debes "cambiar" el operador de "Y" a "O" o de "O" a "Y".
Galería de imágenes
-
Las leyes de De Morgan representadas como un circuito con puertas lógicas.
Véase también
En inglés: De Morgan's laws Facts for Kids
