Ley de Planck para niños
La ley de Planck es una regla muy importante en la física moderna que nos ayuda a entender cómo los objetos calientes emiten luz y calor. Imagina que tienes un objeto que absorbe toda la luz que le llega y, al calentarse, también emite luz. A este objeto ideal lo llamamos "cuerpo negro". La ley de Planck describe exactamente la radiación electromagnética (que incluye la luz visible, el calor infrarrojo y otras ondas) que emite un "cuerpo negro" cuando está a una temperatura específica y en un estado de equilibrio térmico (es decir, su temperatura es constante y bien distribuida).
Esta ley fue un gran avance y es uno de los pilares de la teoría cuántica, que estudia el mundo a escalas muy pequeñas.
Contenido
Historia de la Ley de Planck
Esta ley fue propuesta por el famoso científico Max Planck en el año 1900. Fue un momento clave en la historia de la ciencia, porque Planck tuvo que introducir la idea de que la energía se emite en "paquetes" o "cuantos", lo que fue una idea revolucionaria.
¿Cómo se aplica la Ley de Planck?
La ley de Planck nos ayuda a entender la luz y el calor que emiten diferentes objetos en el universo.
El Sol y su radiación
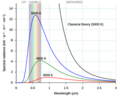
Si aplicamos la ley de Planck al Sol, que tiene una temperatura en su superficie de unos 6000 grados K, descubrimos cosas interesantes:
- Casi toda la luz y el calor que emite el Sol (el 99%) se encuentra en un rango de longitud de ondas entre 0.15 micrómetros (μm) y 4 micrómetros.
- El punto donde el Sol emite más energía es a 0.475 micrómetros.
- Para que te hagas una idea, 1 nanómetro (nm) es una mil millonésima parte de un metro (10-9 m). Así, el Sol emite luz en un rango de 150 nm a 4000 nm, y su máximo está en 475 nm.
- La luz que podemos ver con nuestros ojos se encuentra entre los 380 nm y los 740 nm. Esto significa que el Sol emite mucha luz visible.
- También emite radiación ultravioleta (ondas más cortas) desde 150 nm hasta 380 nm, y radiación infrarroja (ondas más largas, que sentimos como calor) desde 0.74 μm hasta 4 μm.
La Tierra y su radiación
La Tierra también emite radiación, pero como está mucho más fría que el Sol, la radiación que emite es diferente:
- Con una temperatura superficial de unos 288 K (que son unos 15 °C), el 99% de la radiación que emite la Tierra está entre 3 μm y 80 μm.
- El máximo de emisión de la Tierra ocurre a 10 μm. Esto significa que la Tierra emite principalmente radiación infrarroja, que es el calor que sentimos.
- Incluso la estratosfera de la Tierra, que está entre 210 K y 220 K, irradia entre 4 μm y 120 μm, con un máximo en 14.5 μm.
Descripción de la Ley de Planck
La ley de Planck se expresa con una fórmula matemática que relaciona la energía emitida por un cuerpo negro con su temperatura y la frecuencia o longitud de onda de la radiación. Esta fórmula nos permite calcular cuánta energía emite un objeto a una temperatura dada en cada tipo de onda.
Intensidad de la radiación
La intensidad de la radiación, también llamada radiancia espectral, nos dice cuánta energía emite un cuerpo negro por cada unidad de área, por unidad de tiempo y en una dirección específica, para un rango de frecuencias. Es como medir el "brillo" de un objeto en diferentes colores o tipos de luz.
Flujo de radiación
El flujo de radiación, o poder emisivo espectral, es la cantidad total de energía radiante que un cuerpo emite por unidad de superficie y por unidad de tiempo, en un rango específico de frecuencias. Es una medida de la energía total que sale de la superficie de un objeto.
De la ley de Planck se derivan otras leyes importantes de la física, como la ley de Stefan-Boltzmann y la ley de desplazamiento de Wien.
- La ley de desplazamiento de Wien nos dice en qué longitud de onda se produce el máximo de emisión de un cuerpo (por ejemplo, por qué el Sol brilla en amarillo y no en azul).
- La ley de Stefan-Boltzmann nos dice la potencia total de energía que emite un cuerpo por unidad de área.
Por eso, a medida que un objeto se calienta, su brillo cambia de color: primero se pone rojo, luego amarillo y, si se calienta mucho, puede llegar a ser azul o blanco.
Unidades de Medida
En el Sistema Internacional de Unidades (también conocido como sistema MKS), la longitud de onda se mide en metros (m). El poder emisivo (la energía emitida) se mide en vatios por metro cuadrado (W/m²), y el poder emisivo por unidad de longitud de onda se mide en vatios por metro cúbico (W/m³).
Sin embargo, para la luz y el calor, a menudo es más práctico usar unidades más pequeñas:
- Los nanómetros (nm) son muy útiles para medir las longitudes de onda de la luz visible y ultravioleta (1 nm = 10-9 m).
- Los micrómetros (μm), también llamados micras, son comunes para medir las longitudes de onda de la radiación infrarroja (1 μm = 10-6 m).
Galería de imágenes
-
Ley de Planck para cuerpos a diferentes temperaturas.
-
Curvas de emisión de cuerpos negros a diferentes temperaturas comparadas con las predicciones de la física clásica anteriores a la ley de Planck.
Véase también
En inglés: Planck's law Facts for Kids
- Max Planck
- Unidades de Planck
- Constante de Planck
- Ley de Stefan-Boltzmann
- Ley de desplazamiento de Wien
- Aproximación de Wien
- Catástrofe ultravioleta
- Mecánica cuántica
- Radiación térmica
- Radiación solar
- Radiación terrestre
