Ley de Stefan-Boltzmann para niños
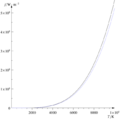
La ley de Stefan-Boltzmann nos ayuda a entender cómo los objetos calientes emiten energía en forma de calor y luz. Esta ley dice que la cantidad total de energía que un objeto emite por segundo y por metro cuadrado es proporcional a la cuarta potencia de su temperatura. Esto significa que si un objeto se calienta un poco, ¡la energía que emite aumenta muchísimo!
Esta ley funciona de manera muy precisa para objetos ideales llamados cuerpos negros. Un cuerpo negro es un objeto teórico que absorbe toda la radiación que le llega y emite la máxima cantidad de radiación posible para su temperatura. Aunque no existen cuerpos negros perfectos en la realidad, esta ley es una buena aproximación para la mayoría de los objetos, a los que llamamos "cuerpos grises".
Contenido
Historia de la Ley de Stefan-Boltzmann
¿Quién descubrió esta ley?
La ley fue propuesta por primera vez en 1879 por el físico austriaco Josef Stefan. Él llegó a esta conclusión estudiando los resultados de experimentos que había hecho otro físico, John Tyndall. Stefan publicó sus hallazgos en un artículo llamado «Sobre la relación entre la radiación térmica y la temperatura».
¿Cómo se demostró la ley?
Unos años después, en 1884, otro físico austriaco, Ludwig Boltzmann, demostró esta ley usando principios de la termodinámica. La termodinámica es la rama de la física que estudia el calor y la energía. Boltzmann imaginó un motor especial que usaba luz en lugar de gas para funcionar, y así pudo confirmar la ley de Stefan de forma teórica. Por eso, la ley lleva el nombre de ambos científicos.
¿Cómo funciona la ley de Stefan-Boltzmann?
La ley se expresa con una fórmula sencilla: 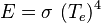
Aquí te explicamos qué significa cada parte:
- E es la energía total que el objeto emite por segundo y por metro cuadrado. Se mide en vatios por metro cuadrado (W/m²).
- Te es la temperatura efectiva del objeto, medida en kelvin (K). Es muy importante usar la temperatura en kelvin, que es una escala de temperatura absoluta.
- σ (sigma) es un número especial llamado constante de Stefan-Boltzmann. Su valor es aproximadamente 5.67 x 10-8 W/(m² K⁴).
Esta fórmula nos dice la energía máxima que un objeto puede emitir a una temperatura dada, como si fuera un cuerpo negro ideal.
¿Qué pasa con los objetos reales?
Los objetos reales no son cuerpos negros perfectos, así que emiten un poco menos de energía. Para calcular la energía que emite una superficie real, usamos una pequeña modificación de la fórmula:
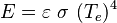
Aquí, ε (épsilon) es la emisividad. La emisividad es un número que nos dice qué tan bien un objeto real emite radiación en comparación con un cuerpo negro. Su valor está entre 0 y 1. Si un objeto tiene una emisividad de 1, es un cuerpo negro perfecto. Si tiene una emisividad de 0, no emite nada de radiación. La emisividad depende del material del objeto, de cómo está su superficie (si es lisa o rugosa) y de su temperatura.
Ejemplos de la Ley de Stefan-Boltzmann en acción
¿Cómo se calculó la temperatura del Sol?
Uno de los primeros usos importantes de esta ley fue para calcular la temperatura de la superficie del Sol. Josef Stefan usó datos de un científico llamado Charles Soret, quien había medido que la energía que llega del Sol es unas 29 veces mayor que la de una placa de metal caliente.
Stefan estimó que la placa de metal estaba a unos 1900 °C o 2000 °C. También consideró que la atmósfera terrestre absorbe parte de la energía del Sol. Con estos datos y su ley, Stefan calculó que la temperatura de la superficie del Sol era de aproximadamente 5713 K (unos 5440 °C). ¡Este valor es muy cercano al valor moderno, que es de 5780 K! Antes de esto, las estimaciones de la temperatura del Sol variaban mucho, desde 1800 °C hasta 13,000,000 °C.
¿Cómo se miden las estrellas?
Los astrónomos usan la ley de Stefan-Boltzmann para calcular la temperatura y el tamaño de las estrellas. Suponen que las estrellas emiten radiación de manera similar a un cuerpo negro. La luminosidad (la energía total que emite una estrella por segundo) se calcula con esta fórmula:
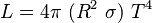
Donde:
- L es la luminosidad de la estrella.
- R es el radio de la estrella.
- T es la temperatura de la superficie de la estrella.
- σ es la constante de Stefan-Boltzmann.
Con esta fórmula, los astrónomos pueden estimar el tamaño de las estrellas si conocen su luminosidad y temperatura.
¿Cuál es la temperatura de la Tierra?
También podemos usar esta ley para calcular la temperatura promedio de la Tierra. La Tierra recibe energía del Sol y, a su vez, emite energía al espacio. Si igualamos la energía que la Tierra recibe del Sol con la energía que emite, podemos estimar su temperatura.
Usando la ley de Stefan-Boltzmann y la distancia entre el Sol y la Tierra, se calcula que la temperatura de la Tierra debería ser de unos 278 K (aproximadamente 5 °C). Sin embargo, la temperatura real promedio de la Tierra es de unos 15 °C.
¿Por qué hay una diferencia? Hay dos razones principales:
- Albedo: Parte de la energía solar que llega a la Tierra es reflejada de vuelta al espacio por las nubes, el hielo y otras superficies brillantes. Esto se llama albedo y hace que la Tierra sea un poco más fría de lo que se calcularía sin considerarlo (llegaría a -18 °C).
- Efecto invernadero: Algunos gases en la atmósfera terrestre, como el dióxido de carbono y el vapor de agua, absorben parte de la energía que la Tierra irradia. Estos gases actúan como una manta, atrapando el calor y calentando la atmósfera. Este fenómeno se conoce como efecto invernadero y es vital para que la vida pueda existir en nuestro planeta.
Galería de imágenes
Véase también
 En inglés: Stefan–Boltzmann law Facts for Kids
En inglés: Stefan–Boltzmann law Facts for Kids