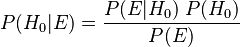Inferencia bayesiana para niños
La inferencia bayesiana es una forma especial de estadística que nos ayuda a entender y actualizar nuestras creencias sobre algo. Imagina que tienes una idea o una hipótesis sobre cómo funciona el mundo. Con la inferencia bayesiana, usamos nuevas evidencias o información para cambiar y mejorar esa idea inicial.
Esta forma de pensar lleva el nombre del matemático Thomas Bayes, quien desarrolló un teorema muy importante. El teorema de Bayes es como la regla principal que usamos para hacer estos ajustes en nuestras creencias. Hoy en día, la inferencia bayesiana se usa en muchos campos, como la teoría de la decisión (para tomar mejores decisiones), la visión artificial (para que las computadoras "vean" y entiendan imágenes) y el reconocimiento de patrones (para identificar cosas en datos).
Contenido
¿Cómo funciona la Inferencia Bayesiana?
La importancia de la incertidumbre
En la vida real, no siempre estamos 100% seguros de todo. A veces, la información es incierta o un poco imprecisa. La lógica tradicional suele decir que algo es verdadero o falso, sin puntos intermedios. Pero la inferencia bayesiana es diferente. Nos permite trabajar con la incertidumbre y la imprecisión.
Los métodos bayesianos nos dan una forma de medir qué tan probable es que una hipótesis sea cierta, incluso cuando no tenemos toda la información. Es como asignar un "nivel de confianza" a nuestras ideas. Cuando obtenemos nuevas pruebas, este nivel de confianza se actualiza.
Actualizando nuestras creencias con pruebas
La inferencia bayesiana es muy parecida a cómo funciona el método científico. En la ciencia, los investigadores recogen evidencia para ver si sus hipótesis son correctas. A medida que se acumulan más pruebas, nuestra confianza en una hipótesis puede aumentar mucho o disminuir mucho.
Si tenemos suficiente evidencia, podemos llegar a creer que una hipótesis es muy probable o muy poco probable. Así, la inferencia bayesiana nos ayuda a decidir entre diferentes ideas: las que tienen un nivel de confianza muy alto se consideran más cercanas a la verdad, y las que tienen un nivel muy bajo se descartan.
Sin embargo, es importante saber que nuestras creencias iniciales (antes de ver cualquier evidencia) pueden influir en el resultado. Por eso, es bueno ser conscientes de nuestros propios puntos de partida.
Un ejemplo sencillo de Inferencia Bayesiana
Imagina el siguiente ejemplo:
- Durante miles de millones de años, el sol siempre ha salido después de haberse puesto. El sol se puso esta noche. Por lo tanto, hay una probabilidad muy, muy alta de que el sol vuelva a salir mañana. Y hay una probabilidad muy, muy baja de que el sol no salga mañana.
Este ejemplo muestra cómo usamos la experiencia pasada (la evidencia de miles de millones de años) para formar una creencia sobre un evento futuro. La inferencia bayesiana usa números para representar este "grado de creencia" antes de ver la evidencia y luego lo recalcula después de verla.
Las partes de la fórmula de Bayes
Aunque la fórmula puede parecer complicada, sus partes son bastante lógicas. El teorema de Bayes nos ayuda a ajustar la probabilidad de una hipótesis cuando tenemos nueva evidencia.
La fórmula básica es:
Vamos a ver qué significa cada parte:
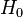representa nuestra hipótesis (la idea que queremos probar).
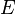es la nueva evidencia o información que hemos observado.
Probabilidad antes y después de la evidencia
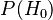se llama la probabilidad a priori de 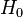. Es nuestra creencia inicial sobre la hipótesis antes de ver la nueva evidencia.
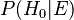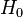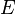se llama la probabilidad a posteriori de dado . Es nuestra creencia actualizada sobre la hipótesis DESPUÉS de haber visto la nueva evidencia.
¿Qué es la "verosimilitud"?
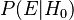se llama la probabilidad condicional de que la evidencia 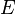ocurra si la hipótesis 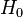es verdadera. También se le llama función de verosimilitud. Nos dice qué tan probable es ver la evidencia si nuestra hipótesis es correcta.
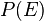se llama la probabilidad marginal de 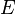. Es la probabilidad total de observar la nueva evidencia 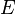, considerando todas las posibles hipótesis.
El factor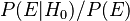 
nos muestra cuánto impacto tiene la nueva evidencia en nuestra creencia en la hipótesis. Si es muy probable ver la evidencia cuando la hipótesis es verdadera, este factor será grande. Al multiplicar nuestra creencia inicial por este factor, obtenemos una creencia actualizada más fuerte. En resumen, el teorema de Bayes mide cuánto la nueva evidencia puede cambiar nuestra confianza en una hipótesis.
¿Para qué se usa la Inferencia Bayesiana?
La inferencia bayesiana es una herramienta muy útil para tomar decisiones. Se usa, por ejemplo, en la teoría de la decisión para calcular probabilidades y evaluar riesgos. Esto ayuda a entender las posibles consecuencias de cometer un error.
También se puede aplicar la inferencia bayesiana varias veces. Si tenemos varias evidencias independientes, podemos usar la primera evidencia para actualizar nuestra creencia, luego usar esa creencia actualizada como punto de partida para la siguiente evidencia, y así sucesivamente.
Galería de imágenes
Véase también
En inglés: Bayesian inference Facts for Kids
- Teorema de Bayes
- Inferencia bayesiana en filogenia
- Razonamiento abductivo
- Epistemología bayesiana
- Análisis de sensibilidad (estadística)
- Optimización de hiperparámetros
