Homología (matemática) para niños
La homología es una herramienta matemática que nos ayuda a entender la forma de los objetos, especialmente los espacios topológicos. Imagina que quieres describir un objeto sin tocarlo, solo por sus "agujeros". La homología nos permite hacer eso, asociando a cada objeto una serie de grupos de números que nos dicen cuántos y de qué tipo son sus agujeros.
Por ejemplo, piensa en una dona y una pelota. Una dona tiene un agujero en el centro, mientras que una pelota no tiene agujeros que la atraviesen. La homología nos ayuda a distinguir estas formas de manera precisa. Es como una forma de "contar" los agujeros de un objeto en diferentes dimensiones.
Los grupos de homología son más fáciles de calcular que otros métodos matemáticos para clasificar formas, lo que los hace muy útiles para los científicos y matemáticos.
Contenido
¿Qué son los agujeros en matemáticas?
Para entender la homología, primero debemos pensar en qué significa un "agujero" en el mundo de las matemáticas. No es un agujero físico como el de una pared, sino una característica de la forma de un objeto.
Agujeros en diferentes dimensiones
- Un Círculo tiene un agujero en su centro. Si lo cortas, se convierte en una línea. Este es un agujero de una dimensión.
- Una Esfera (como la superficie de una pelota) no tiene agujeros que la atraviesen. Cualquier lazo que dibujes en ella se puede encoger hasta un punto.
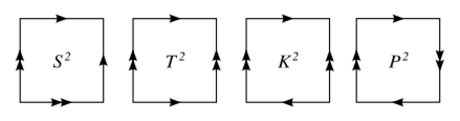
- Una Dona (matemáticamente llamada toro) tiene un agujero en el centro, como el círculo, pero también tiene un agujero que la rodea. Si cortas la dona de cierta manera, puedes "desenrollarla" en un cuadrado.
La homología nos ayuda a definir y clasificar estos "agujeros" de manera formal.
Ciclos y fronteras
Para entender los agujeros, la homología usa ideas como:
- Ciclos: Son como caminos cerrados o superficies cerradas dentro de un objeto. Piensa en un lazo dibujado en una superficie.
- Fronteras: Son ciclos que, en realidad, son el borde de algo más grande dentro del objeto. Por ejemplo, el borde de un disco es un ciclo, pero como es el borde de un disco, se considera una frontera.
Un agujero existe cuando tienes un ciclo que no es la frontera de nada dentro del objeto. Los grupos de homología nos dicen cuántos de estos ciclos "verdaderos" hay y cómo se relacionan entre sí.
Historia de la homología
La idea de la homología tiene raíces antiguas, pero se desarrolló formalmente hace poco más de un siglo.
Primeros pasos
La historia de la homología comienza con el matemático Leonhard Euler, quien en el siglo XVIII descubrió una fórmula para los poliedros (figuras 3D con caras planas, como un cubo). Esta fórmula, conocida como la característica de Euler, relaciona el número de vértices, aristas y caras de un poliedro.
Más tarde, en el siglo XIX, matemáticos como Bernhard Riemann y Enrico Betti continuaron explorando cómo describir las formas de los objetos usando números. Betti demostró que ciertos números, que hoy llamamos "números de homología", son propiedades fijas de un objeto, sin importar cómo lo dibujemos o lo deformemos sin romperlo.
El trabajo de Poincaré
El matemático francés Henri Poincaré fue quien desarrolló la primera teoría completa de la homología a finales del siglo XIX. En su trabajo "Analysis situs" (que significa "análisis de la posición"), Poincaré introdujo las ideas de ciclos y relaciones entre ellos para clasificar las formas de los objetos. Él mostró cómo los "números de Betti" (que son un refinamiento de la característica de Euler) y la "torsión" (una propiedad que veremos más adelante) nos dan una descripción completa de los agujeros de un objeto.
Desarrollo moderno
En el siglo XX, matemáticos como Emmy Noether y Leopold Vietoris y Walther Mayer llevaron la homología al campo del álgebra. Esto permitió estudiar las formas de los objetos usando herramientas de grupos matemáticos, haciendo la teoría más rigurosa y poderosa. Hoy en día, la homología algebraica es una de las principales herramientas para clasificar y entender las formas complejas.
Ejemplos de superficies y sus agujeros
Veamos cómo la homología nos ayuda a entender diferentes superficies.
La esfera
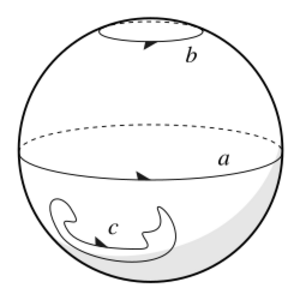
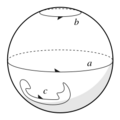
En una Esfera (como la superficie de una pelota), cualquier lazo cerrado que dibujes puede ser encogido hasta un solo punto. Esto significa que la esfera no tiene agujeros "verdaderos" que la atraviesen. Si cortas una esfera a lo largo de un lazo, siempre la dividirás en dos partes.
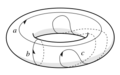
El toro (dona)
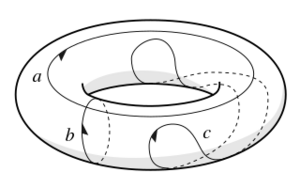
El toro (la superficie de una dona) es diferente. Tiene lazos que no se pueden encoger a un punto. Por ejemplo, un lazo que rodea el agujero central de la dona o un lazo que la atraviesa por el centro. Estos lazos representan los agujeros del toro. Si cortas el toro a lo largo de estos lazos, puedes "desenrollarlo" y aplanarlo en un cuadrado.
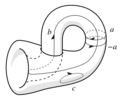
La botella de Klein
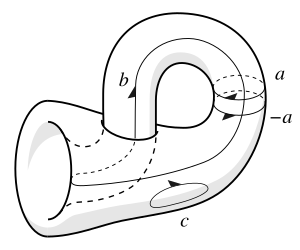
La Botella de Klein es una superficie muy curiosa que no tiene "adentro" ni "afuera". Es como un toro, pero con un "giro" especial. Si intentas dibujar un lazo en ella y lo sigues, puedes terminar en el lado "opuesto" de donde empezaste, ¡aunque no haya lados opuestos! Esto se debe a que la botella de Klein no es "orientable", lo que significa que no puedes definir consistentemente una dirección de "izquierda" o "derecha" en toda su superficie.
El plano proyectivo
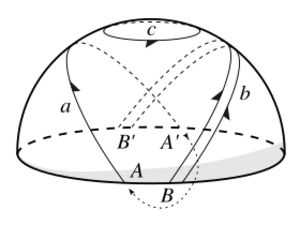
El Plano proyectivo es otra superficie interesante. Se puede pensar como una esfera donde los puntos opuestos (antípodas) se consideran el mismo punto. Al igual que la botella de Klein, no es orientable.
Uniendo y cortando ciclos
En homología, podemos "sumar" o "restar" ciclos. Por ejemplo, si cortas una superficie a lo largo de un lazo y luego lo vuelves a pegar, es como si no hubieras hecho nada. Esto se representa como la suma de un ciclo y su opuesto siendo igual a cero.
En la botella de Klein, si sigues un lazo dos veces, puedes terminar en el mismo lugar pero con una orientación invertida. Esto es un ejemplo de "torsión", una propiedad que nos dice que un ciclo debe ser recorrido varias veces para que se "cierre" o se vuelva trivial.
Homología vs. homotopía
La homología y la homotopía son dos formas de estudiar los agujeros en los espacios topológicos.
Similitudes y diferencias
- Ambas nos ayudan a identificar "agujeros".
- Los grupos de homología son generalmente más fáciles de calcular.
- Los grupos de homotopía pueden ser más complejos y capturar más detalles sobre cómo los lazos se pueden deformar en un espacio.
Imagina que tienes una figura en forma de "8". Su grupo de homotopía distingue si recorres primero el lazo izquierdo y luego el derecho, o viceversa, porque el orden importa. Sin embargo, su grupo de homología solo se preocupa por los "cortes" que puedes hacer. Cortar el lazo izquierdo y luego el derecho es lo mismo que cortar el derecho y luego el izquierdo, porque el orden de los cortes no cambia el resultado final de la superficie. Por eso se dice que "la homología es una alternativa conmutativa a la homotopía", lo que significa que el orden de las operaciones no importa.
Galería de imágenes
-
Ciclos en 2 esferas
-
Ciclos en un toro
-
Ciclos en una botella de Klein
-
Ciclos en un plano proyectivo hemisférico
-
Las cuatro formas de pegar un cuadrado para hacer una superficie cerrada: pegar flechas sencillas y pegar flechas dobles de forma que las puntas de las flechas apunten en la misma dirección.
Véase también
En inglés: Homology (mathematics) Facts for Kids
- Álgebra homológica
- Cohomología
- Número de Betti
- Grupo de homotopía
