Forma del universo para niños
La forma del universo es un tema fascinante que los científicos estudian para entender cómo es nuestro universo en su totalidad. Los expertos en cosmología física, que es la ciencia que investiga el origen, la evolución y el futuro del universo, quieren saber cómo es su geometría.
Para entender la forma del universo, los científicos lo dividen en dos partes:
- La geometría local: Se refiere a la forma de la parte del universo que podemos observar.
- La geometría global: Intenta describir la forma de todo el universo, incluso más allá de lo que podemos ver.
Este estudio incluye conceptos como la curvatura y la topología, que nos ayudan a comprender mejor el espacio.
Contenido
Geometría local: ¿Cómo es el espacio a nuestro alrededor?
La geometría local se refiere a la curvatura del espacio en cualquier punto del universo que podemos observar. Imagina que el espacio no es siempre "plano" como una hoja de papel, sino que puede curvarse.
Los científicos han hecho muchas observaciones, como las de las supernovas (estrellas que explotan) y la radiación de fondo de microondas (un "eco" del Big Bang). Estas observaciones muestran que el universo observable es bastante uniforme y se está expandiendo cada vez más rápido.
Para describir esto, los científicos usan un modelo matemático llamado métrica de Friedman-Lemaître-Robertson-Walker (FLRW). Este modelo nos ayuda a entender la curvatura del universo, tratando la materia como un fluido.
Otra forma de entender la geometría local es midiendo la cantidad de materia que hay en el universo. Si ignoramos la energía oscura y asumimos que la materia está distribuida de manera uniforme, podemos determinar la curvatura. Las observaciones confirman que, aunque hay zonas con más materia (como las galaxias), en general el universo es muy uniforme.
Un concepto importante es el parámetro de densidad, llamado Omega (Ω). Omega es la densidad promedio del universo dividida por la densidad necesaria para que el universo sea "plano" (sin curvatura).
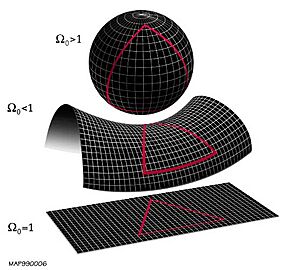
- Si Ω = 1, la curvatura es cero, y el teorema de Pitágoras (a² + b² = c²) funciona perfectamente en el espacio.
- Si Ω > 1, hay una curvatura positiva. Imagina la superficie de una esfera. En este caso, el teorema de Pitágoras no sería exacto para distancias muy grandes.
- Si Ω < 1, hay una curvatura negativa. Imagina una silla de montar. Aquí, el teorema de Pitágoras tampoco sería exacto para distancias muy grandes.
Las mediciones actuales de la materia y la energía en el universo, usando eventos como las supernovas, sugieren que la curvatura del espacio está muy cerca de cero. Esto significa que, a nivel local, el espacio se parece mucho a la geometría euclidiana (la que aprendemos en la escuela).
Tipos de geometrías locales
Existen tres tipos principales de geometrías para describir la curvatura constante del espacio, dependiendo de si la curvatura es cero, positiva o negativa:
- Si la curvatura es cero, la geometría es plana.
- Si la curvatura es positiva, la geometría es esférica.
- Si la curvatura es negativa, la geometría es hiperbólica.
Para entender estas geometrías, podemos usar un sistema de coordenadas donde la expansión del universo no se tiene en cuenta. Esto nos permite ver el universo como un espacio estático de tres dimensiones.
Asumiendo que el universo es uniforme, la geometría local se describe con una de estas tres formas:
- La geometría euclidiana de 3 dimensiones (E³).
- La geometría esférica de 3 dimensiones (S³).
- La geometría hiperbólica de 3 dimensiones (H³).
Incluso si el universo no es perfectamente plano, su curvatura es tan pequeña que el radio de esa curvatura es mucho mayor que el universo observable.
En la geometría clásica euclidiana, si tienes una línea y un punto fuera de ella, solo puedes dibujar una línea paralela a la primera que pase por ese punto. Además, la suma de los ángulos de cualquier triángulo siempre es 180°.
- En la geometría esférica, por un punto no pasa ninguna línea paralela, y la suma de los ángulos de un triángulo es mayor de 180°.
- En la geometría hiperbólica, por un punto pueden pasar dos o más líneas paralelas, y la suma de los ángulos de un triángulo es menor de 180°.
Geometría global: ¿Cómo es el universo completo?
La geometría global se refiere a la forma de todo el universo, incluyendo su topología. La topología estudia cómo están conectados los puntos en el espacio, sin importar su tamaño o forma.
Aunque la geometría local nos da pistas, no puede determinar por completo la geometría global. Sin embargo, si la curvatura local es constante, esto limita las posibilidades.
Dos preguntas importantes en el estudio de la geometría global son:
- ¿El universo es infinito en tamaño o es un espacio compacto (finito)?
- ¿El universo tiene una topología simple o no simple (es decir, si tiene "agujeros" o conexiones extrañas)?
¿Es el universo finito o infinito?
Un espacio compacto es como un espacio que tiene un "volumen" o un tamaño definido, como una esfera. En un espacio compacto, si viajas en línea recta en una dirección, eventualmente regresarías al punto de partida.
Si la geometría del universo no es compacta, entonces es infinita. En este caso, si viajas en línea recta, nunca regresarías al punto de partida, y el espacio no tendría un volumen definido, como un plano infinito.
- Si la geometría espacial es esférica, la topología es compacta (finita).
- Si la geometría espacial es plana o hiperbólica, la topología puede ser compacta o infinita.
Universo plano
En un universo plano, tanto la curvatura local como la global son planas. Generalmente, se describe como un espacio euclídeo (como el espacio que conocemos). Sin embargo, también puede ser plano pero limitado en una o más direcciones, como un cilindro, un toro (forma de rosquilla) o una banda de Möbius en dos dimensiones. En tres dimensiones, existen formas similares como la botella de Klein.
Las últimas mediciones de la curvatura del espacio, realizadas por la misión espacial europea Planck, indican que el universo es muy, muy cercano a ser plano.
Universo esférico
Un universo esférico se describe con la geometría esférica. Puedes imaginarlo como una hiperesfera tridimensional, que es como la superficie de una esfera, pero en cuatro dimensiones.
Los científicos han analizado datos de la sonda WMAP (Wilkinson Microwave Anisotropy Probe) para buscar imágenes repetidas del universo distante en la radiación de fondo de microondas. Si el universo fuera finito y la luz tuviera tiempo suficiente para viajar, podríamos ver múltiples imágenes de los mismos objetos. Si el universo es finito, pero las observaciones no muestran estas repeticiones, significa que la curvatura es muy pequeña, como la curvatura de la Tierra en un área pequeña.
Generalmente, la idea de un universo con geometría esférica se asocia con un universo finito (que tiene un tamaño limitado).
Universo hiperbólico
Un universo hiperbólico se describe con la geometría hiperbólica. Puedes imaginarlo como una forma de silla de montar que se extiende infinitamente. A veces se le llama "abierto".
Si el universo es hiperbólico, se cree que se expandirá para siempre, terminando en un estado de "muerte térmica" (donde todo se enfría y se dispersa), un "Gran Congelamiento" o un "Gran Desgarramiento". Aunque también podría terminar en un "Gran Colapso". Esta topología es compatible con las mediciones astrofísicas recientes.
Galería de imágenes
Véase también
 En inglés: Shape of the universe Facts for Kids
En inglés: Shape of the universe Facts for Kids