Espacio vectorial para niños

En álgebra lineal, un espacio vectorial es un conjunto especial de elementos, llamados vectores, donde puedes hacer dos cosas principales: sumarlos entre sí y multiplicarlos por números (a los que llamamos escalares). Pero no es cualquier conjunto; para ser un espacio vectorial, debe cumplir 8 reglas o propiedades muy importantes.

Imagina que tienes un grupo de flechas (vectores) en un plano o en el espacio. Puedes sumar dos flechas para obtener una nueva flecha, y puedes hacer una flecha más larga o más corta (o cambiar su dirección) multiplicándola por un número. Si estas operaciones siguen ciertas reglas, entonces ese conjunto de flechas forma un espacio vectorial.

Representación artística de un espacio vectorial.

La Historia de los Espacios Vectoriales

Las ideas que llevaron a los espacios vectoriales que conocemos hoy comenzaron hace mucho tiempo, en el siglo XVII. En esa época, matemáticos como Descartes y Fermat crearon la geometría analítica. Esto significaba que podían usar números (coordenadas) para describir puntos y líneas en un plano o en el espacio.

Más tarde, en el siglo XIX, el matemático italiano Giuseppe Peano fue el primero en dar una definición clara y moderna de lo que es un espacio vectorial, con todas sus reglas. Otros matemáticos como Grassmann y Cayley también hicieron contribuciones importantes, desarrollando ideas sobre cómo combinar vectores y usar matrices.

Los espacios vectoriales se volvieron muy útiles en una parte de las matemáticas llamada análisis funcional. Aquí, se usan para estudiar funciones y cómo se comportan, por ejemplo, si se acercan a un valor específico (convergencia).

Hoy en día, los espacios vectoriales se usan en muchas áreas, como la ciencia y la ingeniería. Por ejemplo, son clave en la compresión de imágenes y sonido (como las series de Fourier) y para resolver problemas complejos en física.

¿Qué son los Vectores y Escalares?

En un espacio vectorial, los elementos principales son:

• Los vectores: Son los elementos del conjunto principal, como las flechas que mencionamos antes. Se suelen escribir con una flecha encima (como 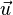) o en negrita (como u).
• Los escalares: Son los números que usamos para multiplicar los vectores. Pueden ser números reales o complejos. Se suelen escribir con letras normales (como o ).

Las Reglas del Juego: Propiedades Clave

Para que un conjunto sea un espacio vectorial sobre un conjunto de números 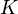(como los números reales), debe cumplir estas 8 propiedades con sus dos operaciones: la suma de vectores y la multiplicación por un escalar.

Suma de Vectores

La suma de dos vectores (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} + \mathbf{v} ) siempre debe dar como resultado otro vector dentro del mismo conjunto .

• Propiedad Conmutativa: El orden de la suma no importa.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}

• Propiedad Asociativa: Si sumas tres vectores, no importa cómo los agrupes.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} + (\mathbf{v} + \mathbf{w}) = (\mathbf{u} + \mathbf{v}) + \mathbf{w}

• Elemento Neutro (Vector Cero): Existe un vector especial, llamado vector cero (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{0} ), que al sumarlo a cualquier vector, no lo cambia.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} + \mathbf{0} = \mathbf{u}

• Elemento Opuesto: Para cada vector 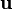, existe otro vector llamado su opuesto (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -\mathbf{u} ), que al sumarlos, dan el vector cero.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} + (-\mathbf{u}) = \mathbf{0}

Multiplicación por un Número (Escalar)

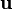Cuando multiplicas un número () por un vector (), el resultado (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot \mathbf{u} ) también debe ser un vector dentro del mismo conjunto .

• Propiedad Asociativa: Si multiplicas un vector por dos números, puedes agrupar los números primero.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot (b \cdot \mathbf{u}) = (a \cdot b) \cdot \mathbf{u}

• Elemento Neutro (Escalar Uno): Existe un número especial, el 1, que al multiplicarlo por cualquier vector, no lo cambia.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 \cdot \mathbf{u} = \mathbf{u}

• Propiedad Distributiva (respecto a la suma de vectores): Puedes "repartir" la multiplicación de un número por la suma de dos vectores.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot (\mathbf{u} + \mathbf{v}) = a \cdot \mathbf{u} + a \cdot \mathbf{v}

• Propiedad Distributiva (respecto a la suma de escalares): Puedes "repartir" la multiplicación de un vector por la suma de dos números.

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a + b) \cdot \mathbf{u} = a \cdot \mathbf{u} + b \cdot \mathbf{u}

Ejemplos Sencillos de Espacios Vectoriales

Para entender mejor, veamos algunos ejemplos comunes de espacios vectoriales.

Vectores en el Plano (R2)

El ejemplo más fácil es el de los vectores en un plano, como los que usas en física para representar fuerzas o movimientos. Cada vector es un par de números Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (u_x, u_y) .

• Suma: Si tienes Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} = (u_x, u_y) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v} = (v_x, v_y) , su suma es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} + \mathbf{v} = (u_x + v_x, u_y + v_y) .
• Multiplicación por un escalar: Si tienes un número y un vector Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} = (u_x, u_y) , el resultado es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot \mathbf{u} = (a \cdot u_x, a \cdot u_y) .

Este conjunto de vectores con estas operaciones cumple las 8 reglas, ¡así que es un espacio vectorial! Lo mismo ocurre con los vectores en el espacio tridimensional ().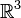

Polinomios

Los polinomios, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(x) = 3x^2 + 2x - 5 , también forman un espacio vectorial.

• Suma: Sumas polinomios sumando los términos con la misma potencia de . Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x^2 + 2x) + (3x^2 - x) = 4x^2 + x .
• Multiplicación por un escalar: Multiplicas cada término del polinomio por el número. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \cdot (x^2 + 2x) = 2x^2 + 4x .

Estas operaciones cumplen las reglas, así que los polinomios son un espacio vectorial.

Matrices

Las matrices (tablas de números) de un tamaño fijo, por ejemplo, matrices de 2x2, también forman un espacio vectorial.

• Suma: Sumas las matrices sumando los números en la misma posición.
• Multiplicación por un escalar: Multiplicas cada número de la matriz por el escalar.

Estas operaciones también cumplen las 8 reglas.

Subespacios Vectoriales: Pequeños Mundos Dentro de Otros

Imagina que tienes un espacio vectorial grande, como todos los vectores en 3D. Un subespacio vectorial es un conjunto más pequeño de vectores dentro de ese espacio grande que, por sí mismo, también es un espacio vectorial. Para que un subconjunto 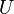de un espacio vectorial sea un subespacio, debe cumplir dos cosas: 1. Si sumas dos vectores de 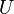, el resultado debe seguir estando en 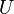. 2. Si multiplicas un vector de 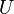por un escalar, el resultado debe seguir estando en 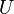. Si cumple esto, entonces 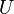es un "pequeño mundo" vectorial dentro de .

Combinaciones Lineales: Mezclando Vectores

Cada vector u es combinación lineal de forma única

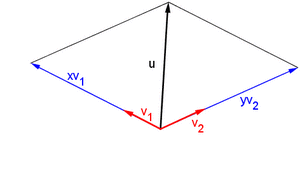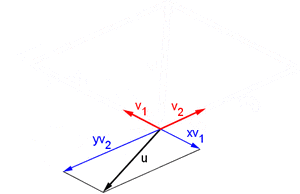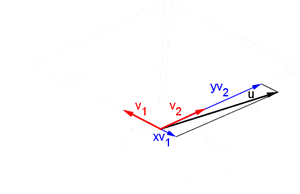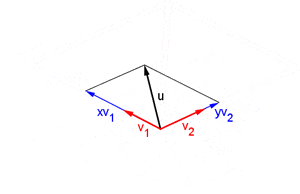
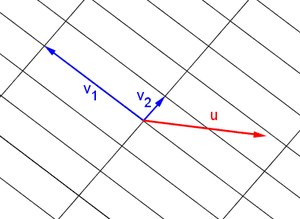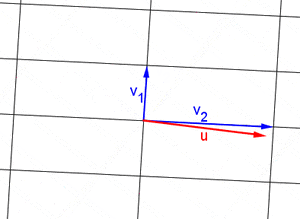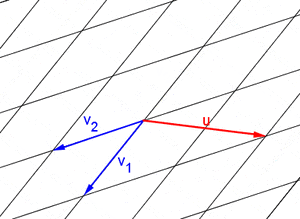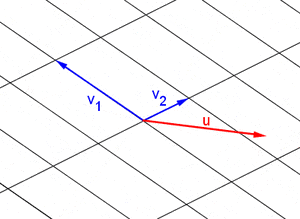
Una combinación lineal es como una receta para crear un nuevo vector usando otros vectores y números. Si tienes un conjunto de vectores Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n\} , una combinación lineal de ellos es un vector que se forma sumándolos después de multiplicarlos por algunos números (escalares). Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} = a_1\mathbf{v}_1 + a_2\mathbf{v}_2 + \dots + a_n\mathbf{v}_n . El conjunto de todos los vectores que puedes crear con una combinación lineal de un grupo de vectores se llama el "espacio generado" por esos vectores.

Independencia Lineal: ¿Son Únicos los Vectores?

Un conjunto de vectores es linealmente independiente si ninguno de ellos puede ser creado como una combinación lineal de los otros. Es decir, si la única forma de que una combinación lineal de ellos dé el vector cero es que todos los números (escalares) sean cero. Si un vector sí se puede crear a partir de los otros, entonces el conjunto es linealmente dependiente. Esto significa que hay "redundancia" en el conjunto.

Bases y Dimensión: El Esqueleto de un Espacio

v₁ y v₂ son base de un plano, si hubiese dependencia lineal (alineados), la cuadrícula no podría generarse.

Una base de un espacio vectorial es un conjunto de vectores que cumple dos condiciones: 1. Son linealmente independientes (no hay redundancia). 2. Generan todo el espacio (puedes crear cualquier vector del espacio con ellos). Una base es como el "esqueleto" o los "ladrillos fundamentales" de un espacio vectorial, porque te permite construir cualquier otro vector de forma única.

La dimensión de un espacio vectorial es simplemente el número de vectores que tiene su base. Por ejemplo:

• El plano (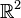) tiene dimensión 2, porque necesitas dos vectores (como (1,0) y (0,1)) para generar cualquier punto en él.
• El espacio 3D (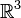) tiene dimensión 3.

Si un espacio tiene una base con un número infinito de vectores, decimos que tiene dimensión infinita.

¿Para Qué Sirven los Espacios Vectoriales?

Los espacios vectoriales son una herramienta muy poderosa en matemáticas y en muchas otras áreas. Permiten estudiar y resolver problemas de una manera más abstracta y general. Por ejemplo:

• En la física, se usan para describir fuerzas, velocidades y campos.
• En la informática, son fundamentales para los gráficos por computadora, el procesamiento de imágenes y el aprendizaje automático.
• En la ingeniería, se aplican en el diseño de estructuras, el análisis de circuitos y la robótica.
• En la economía, se utilizan para modelar sistemas complejos y optimizar recursos.

Son una forma de organizar y entender la información que tiene propiedades de "suma" y "escalado", lo que los hace increíblemente versátiles.

Véase también

En inglés: Vector space Facts for Kids

• Combinación lineal
• Sistema generador
• Independencia lineal
• Base (álgebra)
• Dimensión
• Producto escalar
• Producto vectorial