Coordenadas cartesianas para niños

Las coordenadas cartesianas son un sistema muy útil para ubicar puntos en un mapa o en el espacio. Imagina que tienes una cuadrícula, como la de un juego de batalla naval. Este sistema usa líneas que se cruzan en ángulo recto, como las calles y avenidas de una ciudad.

El nombre "cartesiano" viene de un famoso pensador y matemático francés llamado René Descartes. Él fue quien empezó a usar este método de forma organizada. Gracias a él, podemos describir la posición de cualquier cosa usando números.

Este sistema se puede usar de varias maneras:

• En una línea recta (una dimensión), para ubicar puntos a lo largo de ella.
• En un plano (dos dimensiones), como una hoja de papel, para ubicar puntos con dos números.
• En el espacio (tres dimensiones), para ubicar puntos con tres números.

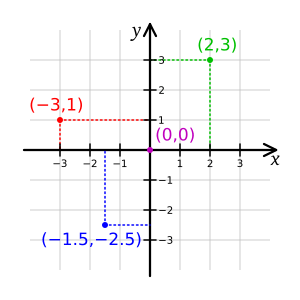
En un plano, las dos líneas principales se llaman ejes. La línea horizontal se conoce como eje X o abscisa, y la línea vertical se llama eje Y o ordenada. Estas líneas se cruzan en un punto central llamado el origen, que es como el punto de partida (0,0).

Tres ejemplos de coordenadas asignadas a tres puntos diferentes (verde, rojo y azul), sus proyecciones ortogonales sobre los ejes constituyen sus coordenadas cartesianas y el origen de coordenadas (0,0) en magenta.

¿Cómo se usan las coordenadas cartesianas?

Las coordenadas cartesianas nos ayudan a dar una dirección exacta a cualquier punto. Por ejemplo, si decimos que un punto está en (2, 3), significa que desde el origen, avanzamos 2 unidades en el eje X (hacia la derecha si es positivo) y 3 unidades en el eje Y (hacia arriba si es positivo). A este par de números (2, 3) se le llama "par ordenado".

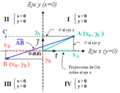
Los cuadrantes del plano

Cuando los dos ejes (X e Y) se cruzan, dividen el plano en cuatro partes, como si fueran las esquinas de una ventana. A estas partes se les llama cuadrantes:

• Primer cuadrante (I): Es la parte de arriba a la derecha. Aquí, los números de X y de Y son ambos positivos (+X, +Y).
• Segundo cuadrante (II): Es la parte de arriba a la izquierda. Aquí, los números de X son negativos y los de Y son positivos (-X, +Y).
• Tercer cuadrante (III): Es la parte de abajo a la izquierda. Aquí, los números de X y de Y son ambos negativos (-X, -Y).
• Cuarto cuadrante (IV): Es la parte de abajo a la derecha. Aquí, los números de X son positivos y los de Y son negativos (+X, -Y).

Sistema de coordenadas cartesianas con un círculo de radio 2 centrado en el origen marcado en rojo. La ecuación de un círculo es (x - a)² + (y - b)² = r² donde a y b son las coordenadas del centro (a, b) y r es el radio.

¿Para qué sirven las coordenadas cartesianas?

Las coordenadas cartesianas son la base de muchas áreas de las matemáticas y la ciencia. Por ejemplo:

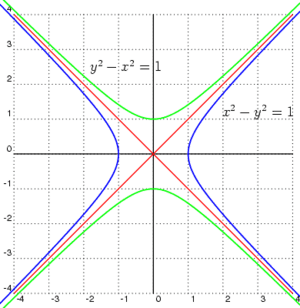
• En la geometría analítica, nos permiten describir figuras geométricas (como líneas, círculos o cuadrados) usando ecuaciones matemáticas.
• En la física, se usan para describir el movimiento de objetos o su posición.
• En la ingeniería, son esenciales para el diseño de estructuras o máquinas.
• En los gráficos por ordenador y el diseño asistido por ordenador (CAD), se usan para crear y manipular imágenes y modelos 3D.

Historia de las coordenadas cartesianas

Las coordenadas cartesianas llevan el nombre de René Descartes (1596-1650), un famoso filósofo y matemático francés. Él tuvo la idea de usar un sistema de referencia para ubicar puntos en un plano. Su objetivo era construir el conocimiento de forma lógica, empezando por un "punto de partida" claro.

Descartes, junto con otro matemático llamado Pierre de Fermat, sentaron las bases de la geometría analítica. Al principio, ellos usaban solo un eje para sus cálculos. La idea de usar un par de ejes perpendiculares (como los conocemos hoy) se popularizó más tarde, después de que la obra de Descartes, La Géométrie, fuera traducida al latín en 1649 por Frans van Schooten y sus estudiantes. Ellos ayudaron a aclarar y expandir las ideas de Descartes.

El desarrollo de este sistema de coordenadas fue muy importante para que otros grandes matemáticos como Isaac Newton y Gottfried Wilhelm Leibniz pudieran desarrollar el cálculo, una rama fundamental de las matemáticas.

Desde entonces, se han creado otros sistemas de coordenadas, como las coordenadas polares (que usan un ángulo y una distancia) o las coordenadas esféricas y cilíndricas para el espacio 3D.

Gráfica de una hipérbola y sus asíntotas.

El plano cartesiano en detalle

En el plano cartesiano, cada punto se identifica con un par de números (x, y). La 'x' es la distancia horizontal desde el eje Y, y la 'y' es la distancia vertical desde el eje X. Estas distancias se miden desde el origen (0,0).

• El eje X se llama también el eje de las abscisas. Su ecuación es y = 0.
• El eje Y se llama también el eje de las ordenadas. Su ecuación es x = 0.

Los ejes dividen el plano en los cuatro cuadrantes que ya mencionamos, donde los signos de las coordenadas cambian. Por ejemplo, en el primer cuadrante, ambas coordenadas son positivas, mientras que en el tercer cuadrante, ambas son negativas.

Distancia entre dos puntos

Con las coordenadas cartesianas, podemos calcular la distancia entre dos puntos. Si tienes un punto A con coordenadas (x_A, y_A) y un punto B con coordenadas (x_B, y_B), la distancia entre ellos se calcula usando una fórmula basada en el teorema de Pitágoras:

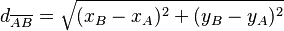
Esta fórmula es como si formaras un triángulo rectángulo con los dos puntos y los ejes, y luego usaras el teorema de Pitágoras para encontrar la longitud de la hipotenusa, que es la distancia entre los puntos.

Coordenadas en el espacio (3D)

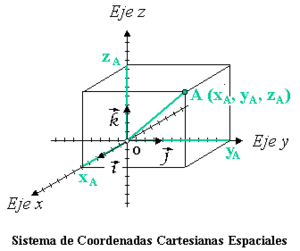
Para ubicar puntos en el espacio tridimensional, necesitamos un tercer eje, el eje Z, que es perpendicular a los ejes X e Y. Así, cada punto en el espacio se "nombra" con tres números: (x, y, z). La 'z' se conoce como la cota.

Coordenadas cartesianas en el espacio 3D.

Los tres planos formados por los ejes (XY, XZ e YZ) dividen el espacio en ocho regiones llamadas octantes. Al igual que en el plano, los signos de las coordenadas (x, y, z) pueden ser positivos o negativos en cada octante.

La distancia entre dos puntos en el espacio 3D también se calcula de forma similar, añadiendo la coordenada z a la fórmula:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d_{\overline{AB}} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2 + (z_B - z_A)^2} \,

Cambios en el sistema de coordenadas

A veces, necesitamos mover o girar nuestro sistema de coordenadas para que sea más fácil trabajar con él. Hay tres transformaciones básicas:

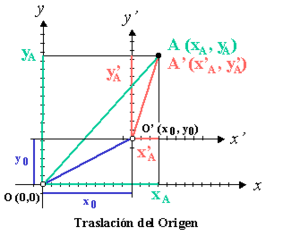
Traslación del origen

Imagina que mueves el punto de origen (0,0) a un nuevo lugar. Si un punto A tiene coordenadas (x_A, y_A) en el sistema original, y el nuevo origen O' está en (x_O', y_O'), las nuevas coordenadas de A (x'_A, y'_A) se calculan restando las coordenadas del nuevo origen:

• x'_A = x_A - x_O'
• y'_A = y_A - y_O'

Esto es como si cambiaras el punto de referencia desde donde mides todo.

Traslación del origen en coordenadas cartesianas.

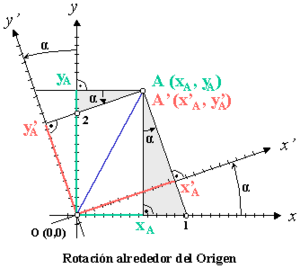
Rotación alrededor del origen

Si giras los ejes X e Y alrededor del origen, las coordenadas de un punto también cambiarán. Si giras los ejes un ángulo α (alfa), las nuevas coordenadas de un punto (x'_A, y'_A) se calculan usando fórmulas que incluyen el seno y el coseno de ese ángulo.

Rotación alrededor del origen en coordenadas cartesianas.

Escalado

El escalado significa que cambias el "tamaño" de la cuadrícula. Si multiplicas las coordenadas de un punto por un factor λ (lambda), el punto se moverá más lejos o más cerca del origen, dependiendo del valor de λ. Por ejemplo, si λ es 2, el punto se alejará el doble del origen.

Galería de imágenes

• 

  Sistema de coordenadas cartesianas.

Véase también

En inglés: Cartesian coordinate system Facts for Kids