Distribución t de Student para niños
Datos para niños Distribución t de student |
||
|---|---|---|
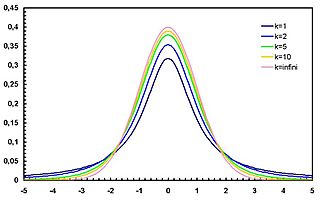 Función de densidad de probabilidad |
||
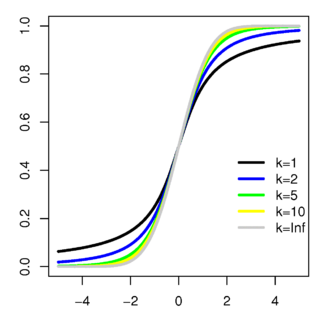 Función de distribución de probabilidad |
||
| Parámetros | 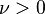 grados de libertad (real) grados de libertad (real) |
|
| Dominio | 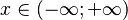 |
|
| Función de densidad (pdf) | 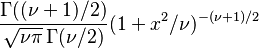 |
|
| Función de distribución (cdf) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{matrix} \frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\[0.5em] \frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2}; -\frac{x^2}{\nu} \right)} {\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)} \end{matrix} donde 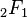 es la función hipergeométrica es la función hipergeométrica |
|
| Media | 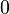 para para 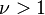 , indefinida para otros valores , indefinida para otros valores |
|
| Mediana | 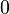 |
|
| Moda | 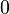 |
|
| Varianza |  para para 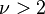 , indefinida para otros valores , indefinida para otros valores |
|
| Coeficiente de simetría | 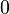 para para 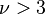 |
|
| Curtosis | 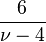 para para  |
|
| Entropía |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{matrix} \frac{\nu+1}{2}\left[ \psi(\frac{1+\nu}{2}) - \psi(\frac{\nu}{2}) \right] \[0.5em] + \log{\left[\sqrt{\nu}B(\frac{\nu}{2},\frac{1}{2})\right]} \end{matrix}
|
|
| Función generadora de momentos (mgf) | (No definida) | |
En el mundo de la probabilidad y la estadística, la distribución t de Student es una herramienta matemática muy útil. Nos ayuda a entender y estimar el promedio de un grupo grande de datos (una población estadística) cuando solo tenemos una pequeña parte de esos datos (una muestra estadística). Es especialmente importante cuando no conocemos la variación total de los datos en la población.
Esta distribución fue creada por un científico llamado William Sealy Gosset en 1908. Él usó el seudónimo «Student» para publicar su trabajo.
La distribución t de Student se usa mucho en pruebas estadísticas, como la "prueba t de Student". Esta prueba nos ayuda a saber si hay diferencias importantes entre dos grupos de datos. También se usa para crear "intervalos de confianza", que son rangos donde es muy probable que se encuentre el verdadero promedio de una población.
Contenido
¿Quién fue Student y por qué es importante su distribución?
La distribución t de Student fue presentada por primera vez en 1908 por William Sealy Gosset. Él era un estadístico que trabajaba en una fábrica de cerveza en Dublín, Irlanda.
Gosset se interesó en cómo analizar datos cuando solo se tenían muestras muy pequeñas. Por ejemplo, quería saber las propiedades químicas de la cebada usando solo unas pocas muestras.
Para publicar sus descubrimientos, Gosset usó el seudónimo «Student». Se dice que su empresa prefería que sus empleados usaran nombres falsos al publicar artículos científicos. Otra razón podría ser que la empresa no quería que sus competidores supieran que estaban usando esta nueva prueba para mejorar la calidad de sus productos.
El trabajo de Gosset se hizo muy conocido gracias a otro científico, Ronald Fisher. Fisher fue quien le dio el nombre de Distribución de Student y usó la letra t para representarla.
¿Cómo funciona la distribución t de Student?
Imagina que quieres saber la altura promedio de todos los estudiantes de tu escuela. Sería muy difícil medir a cada uno. En cambio, podrías tomar una muestra de 30 estudiantes y calcular su altura promedio.
La distribución t de Student nos ayuda a entender qué tan cerca está el promedio de tu muestra del verdadero promedio de todos los estudiantes de la escuela. Es especialmente útil cuando tu muestra es pequeña (menos de 30 datos) y no sabes cuánto varían las alturas en toda la escuela.
¿Qué son los grados de libertad?
Un concepto importante en la distribución t de Student son los "grados de libertad". Piensa en ellos como el número de valores en una muestra que pueden variar libremente. Si tienes 10 datos y ya sabes el promedio, 9 de esos datos pueden ser cualquier número, pero el décimo tiene que ser un valor específico para que el promedio sea el que ya conoces. En este caso, tendrías 9 grados de libertad.
¿Para qué se usa la distribución t de Student?
La distribución t de Student se utiliza en muchas áreas, como:
- Investigación científica: Para comparar los resultados de experimentos con grupos pequeños.
- Control de calidad: Para asegurarse de que los productos cumplen con ciertos estándares, incluso si solo se prueban unas pocas unidades.
- Economía: Para analizar datos económicos cuando no hay mucha información disponible.
Intervalos de confianza: ¿Dónde está el promedio real?
Una de las aplicaciones más comunes de la distribución t de Student es construir "intervalos de confianza". Un intervalo de confianza es un rango de valores donde, con cierta seguridad (por ejemplo, 95% de confianza), se encuentra el verdadero promedio de la población.
Por ejemplo, si calculas la altura promedio de tu muestra de estudiantes y obtienes 1.60 metros, un intervalo de confianza podría decirte que la altura promedio de todos los estudiantes de la escuela está entre 1.58 y 1.62 metros, con un 95% de confianza. Esto es muy útil porque te da una idea de la precisión de tu estimación.
Otras distribuciones relacionadas
La distribución t de Student está relacionada con otras distribuciones importantes en estadística:
- Distribución F: Se usa para comparar las variaciones entre dos o más grupos.
- Distribución χ²: Se utiliza para analizar datos categóricos y para probar si las variaciones observadas en una muestra son similares a las esperadas.
Galería de imágenes
Véase también
 En inglés: Student's t-distribution Facts for Kids
En inglés: Student's t-distribution Facts for Kids


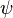 : función digamma,
: función digamma, : función beta
: función beta