Distribución Bernoulli para niños
Datos para niños Bernoulli |
||
|---|---|---|
| Parámetros | 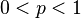 |
|
| Dominio | 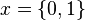 |
|
| Función de probabilidad (fp) | 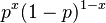 |
|
| Función de distribución (cdf) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{cases} 0 & x<0 \ 1 - p & 0\leq x<1 \ 1 & x\geq 1 \end{cases} | |
| Media | 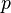 |
|
| Mediana | N/A | |
| Moda | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{cases} 0 & q > p\ 0,1 & q=p\ 1 & q < p \end{cases} | |
| Varianza | 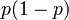 |
|
| Coeficiente de simetría |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{q-p}{\sqrt{pq</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END--> |curtosis = La distribución de Bernoulli es un concepto importante en la teoría de probabilidad y la estadística. Lleva el nombre del matemático suizo Jacob Bernoulli. Esta distribución se usa para describir situaciones donde solo hay dos resultados posibles. Imagina que realizas un experimento una sola vez. Este experimento solo puede tener dos resultados: uno que llamamos "éxito" y otro que llamamos "fracaso". La distribución de Bernoulli nos ayuda a entender la probabilidad de que ocurra el "éxito". Contenido¿Qué es la Distribución de Bernoulli?La distribución de Bernoulli es un modelo matemático para experimentos con solo dos resultados. Piensa en lanzar una moneda: puede salir cara o cruz. O en un examen: puedes aprobar o suspender. Estos son ejemplos perfectos para la distribución de Bernoulli. ¿Quién fue Jacob Bernoulli?Jacob Bernoulli fue un matemático muy importante que vivió en Suiza en el siglo XVII. Fue uno de los primeros en estudiar la probabilidad de manera profunda. Sus ideas sentaron las bases para muchas áreas de las matemáticas y la estadística que usamos hoy. La distribución de Bernoulli es una de sus contribuciones más conocidas. ¿Qué es un Experimento de Bernoulli?Un experimento de Bernoulli, o simplemente un ensayo, es una prueba que cumple con tres condiciones:
Cuando una variable aleatoria (un valor que puede cambiar según el resultado de un experimento) mide el "número de éxitos" en un solo experimento de este tipo, decimos que sigue una distribución de Bernoulli. Se escribe como Ejemplos Sencillos de Experimentos de Bernoulli
¿Cómo se Calcula la Probabilidad en Bernoulli?Para entender la distribución de Bernoulli, usamos dos funciones principales: la función de probabilidad y la función de distribución acumulada. La Función de ProbabilidadLa función de probabilidad nos dice la probabilidad exacta de cada resultado (0 para fracaso, 1 para éxito).
Esto se puede escribir así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{P}[X=x]= \begin{cases} 1-p & \mbox {si }x=0 \\ p & \mbox {si }x=1 \end{cases} La Función de Distribución AcumuladaLa función de distribución acumulada nos dice la probabilidad de que el resultado sea menor o igual a un cierto valor.
Se escribe así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F(x) = \begin{cases} 0 & x<0 \\ 1-p & 0\leq x<1 \\ 1 & x\geq1 \end{cases} Propiedades Clave de la Distribución de BernoulliLa distribución de Bernoulli tiene algunas características importantes que nos ayudan a entenderla mejor. El Valor Esperado (Media)El valor esperado, también conocido como la media o promedio, de una variable de Bernoulli es simplemente la probabilidad de éxito, p. Esto significa que, si repitieras el experimento muchas veces, el promedio de los resultados (donde 1 es éxito y 0 es fracaso) se acercaría a p. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{E}\left[X\right]=p La VarianzaLa varianza nos dice qué tan dispersos están los resultados de un experimento. Para una distribución de Bernoulli, la varianza se calcula como ¿Cómo se Relaciona con la Distribución Binomial?La distribución de Bernoulli es como el "bloque de construcción" de la distribución binomial. Si realizas varios experimentos de Bernoulli independientes (por ejemplo, lanzas una moneda varias veces) y cuentas el número total de éxitos, eso es lo que describe la distribución binomial. En otras palabras, una distribución de Bernoulli es un caso especial de la distribución binomial donde solo se realiza un experimento ( EjemplosEjemplo 1: Lanzar una MonedaImagina que lanzas una moneda y quieres saber la probabilidad de que salga cruz.
La variable aleatoria
Entonces,
Ejemplo 2: Lanzar un Dado y Obtener un 6Ahora, lanzas un dado una sola vez y quieres saber la probabilidad de que salga un 6.
La variable aleatoria
Así,
Véase también
|
|


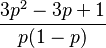 |entropía =
|entropía = 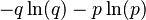 |mgf =
|mgf = 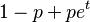 |car =
|car = 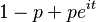 }}
}}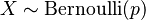 , donde p es la probabilidad de éxito.
, donde p es la probabilidad de éxito. (éxito), la probabilidad es p.
(éxito), la probabilidad es p.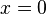 (fracaso), la probabilidad es 1-p.
(fracaso), la probabilidad es 1-p. es menor que 0, la probabilidad acumulada es 0 (no hay resultados posibles).
es menor que 0, la probabilidad acumulada es 0 (no hay resultados posibles).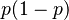 . Una varianza alta significa que los resultados pueden variar mucho, mientras que una baja significa que son más predecibles. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{Var}\left[X\right]= p (1 - p)
. Una varianza alta significa que los resultados pueden variar mucho, mientras que una baja significa que son más predecibles. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{Var}\left[X\right]= p (1 - p)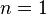 ).
).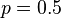 (o 50%).
(o 50%).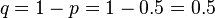 .
. mide el "número de cruces que salen en un lanzamiento".
mide el "número de cruces que salen en un lanzamiento".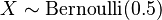 .
.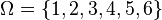 .
.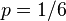 .
.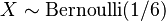 .
. En inglés:
En inglés: