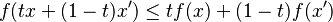Convexidad para niños
La convexidad (del latín convexĭtas, -ātis) de una curva o una superficie, es la zona que se asemeja al exterior de una circunferencia o una superficie esférica, es decir, que tiene su parte sobresaliente dirigida al observador. Es el concepto opuesto a la 'concavidad'.
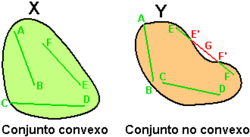
Una parte C de un espacio vectorial real es convexa si para cada par de puntos de C, el segmento que los une está totalmente incluido en C; es decir, un conjunto es convexo si se puede ir de cualquier punto a cualquier otro en línea recta, sin salir del mismo.
Contenido
Definición
Un conjunto 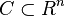 es convexo si para todo
es convexo si para todo 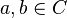 :
:
- el segmento
![[ab] \subset C](/images/math/7/1/a/71a9c971f840204a1682e1e79caa5173.png) .
.
Con otra expresión, ![\forall t \in [0,1]](/images/math/b/0/b/b0bc3797f7ac3371f8e60162ed968567.png) :
:
Nótese que en esta fórmula, la suma de los coeficientes  y
y 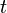 es
es 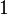 , por lo tanto el punto así definido no depende del origen del sistema de coordenadas.
, por lo tanto el punto así definido no depende del origen del sistema de coordenadas.
En un conjunto no convexo cada segmento que muestra la no convexidad tiene forzosamente que atravesar por lo menos dos veces (en E´y F´) el borde o la frontera del conjunto 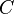 ,
, 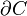 , definida como
, definida como
donde 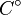 es definido como el interior de
es definido como el interior de 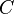 . Por tanto la convexidad depende esencialmente de la forma del borde del conjunto, y la definición equivale a
. Por tanto la convexidad depende esencialmente de la forma del borde del conjunto, y la definición equivale a
donde 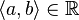 denota el producto escalar usual en
denota el producto escalar usual en 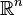 entre
entre  y
y  . Intuitivamente, esto dice que, por cada punto en el borde del conjunto
. Intuitivamente, esto dice que, por cada punto en el borde del conjunto 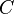 (ósea, cada punto
(ósea, cada punto 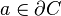 ) existe un vector
) existe un vector 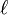 que divide el plano entero, y que cada punto
que divide el plano entero, y que cada punto 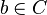 existe solamente en el hiperplano con ángulo que subtiende a ese vector trasladado por
existe solamente en el hiperplano con ángulo que subtiende a ese vector trasladado por  .
.
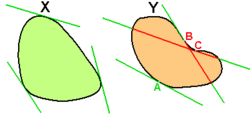
En el caso de una frontera diferenciable (sin puntos angulosos) se pueden considerar sus tangentes (ya que existe un único vector normal a la superficie), y resulta bastante intuitivo que los convexos se caracterizan por hallarse enteramente del mismo lado de cada tangente; es decir que las tangentes nunca atraviesan C (como en el punto A de la figura). Esta propiedad sigue cierta en presencia de puntos angulosos, como en el caso de los polígonos convexos.
Se establece la equivalencia de estas dos caracterizaciones considerando que una tangente (en A por ejemplo) es la posición límite de las cuerdas [AA'] con A' acercándose indefinidamente de A, en el borde de C. El segmento [AA´] está en C mientras que el esto de la recta (AA') está fuera (por el absurdo: si se encuentra un punto B de C en la recta (AA´), fuera de [AA'], entonces el segmento [AB], exterior a C, contradice su convexidad).
Envoltura convexa de un conjunto
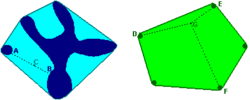
Se llama envolvente convexa de un conjunto dado C al menor (por inclusión) conjunto convexo que contiene a C (es fácil ver que siempre existe). En la figura, la envoltura convexa de la forma azul oscuro es todo el dominio azul (es decir la unión del conjunto original azul oscuro con el dominio azul claro), y la envoltura convexa de los cinco puntos verde oscuro es el polígono verde claro (incluyendo los puntos, por supuesto). En particular, se define
y, como previamente dicho, se nota que, si 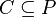 , y
, y  es un conjunto convexo, entonces
es un conjunto convexo, entonces  .
.
Se establece con facilidad que la envoltura convexa es el conjunto de todos los baricentros positivos (es decir con coeficientes todos positivos) de los puntos del conjunto inicial.
En la figura, C es un baricentro positivo de A y B porque está en el segmento [AB], y G es otro tanto de D,E y F, porque se encuentra en el triángulo DEF.
Función convexa
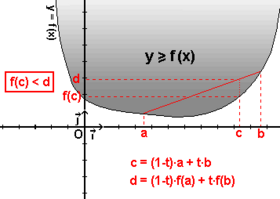
Se dice que una función real, definida sobre un intervalo es convexa si el dominio del plano situado por encima de su curva (en gris en la figura) lo es. Sin sorpresa, las consideraciones anteriores se aplican: Solo importa la frontera del dominio, es decir la curva de ecuación 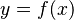 . La convexidad se expresa así: Para cualquier par
. La convexidad se expresa así: Para cualquier par 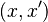 en el intervalo
en el intervalo 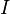 , y cualquier
, y cualquier
Ejemplos: la hipérbola y = 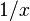 (con x > 0), las parábolas y = ax2 + bx + c, con a > 0 y x real variable, y la función exponencial y = ex. Si la función f es derivable entonces la convexidad equivale a la condición siguiente:
(con x > 0), las parábolas y = ax2 + bx + c, con a > 0 y x real variable, y la función exponencial y = ex. Si la función f es derivable entonces la convexidad equivale a la condición siguiente:
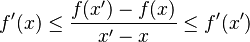
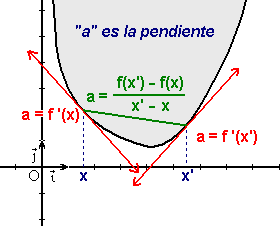
que significa que la pendiente de la cuerda entre dos puntos x y x' está contenida entre los valores extremos de la derivada. Esto equivale al que la derivada sea creciente, en todo el dominio de f . Si f es dos veces derivable, lo anterior significa que la derivada segunda es positiva: f"(x) ≥ 0.
Es fácil verificar que los tres ejemplos anteriores son convexos:
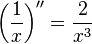
positivo cuando x > 0; (ax2 + bx + c)" = 2a > 0; y (ex)" = ex, siempre positivo.
Equivalentemente, la convexidad de una función puede ser establecida usando lo previamente establecido. Definimos un conjunto
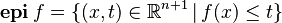
llamado el epigrafo de la función 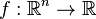 . En este caso, una función es convexa solamente si su epigrafo es un conjunto convexo.
. En este caso, una función es convexa solamente si su epigrafo es un conjunto convexo.
Diferencias entre convexidad y concavidad
La concavidad y la convexidad son definiciones arbitrarias y opuestas. En particular, una función  es cóncava solamente si su inverso aditivo es convexo; es decir,
es cóncava solamente si su inverso aditivo es convexo; es decir,  es cóncava solamente si
es cóncava solamente si 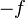 es convexa.
es convexa.
Usando esta definición, solamente funciones afines son tanto cóncavas como convexas. En particular, no es difícil comprobar que si se tiene una función 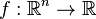 que satisface
que satisface
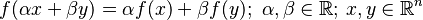
cuando 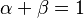 , entonces ambas
, entonces ambas  y
y 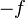 son funciones convexas. El caso contrario también es cierto: si una función es tanto cóncava como convexa, entonces es afín; esta observación se desprende directamente de la definición de convexidad.
son funciones convexas. El caso contrario también es cierto: si una función es tanto cóncava como convexa, entonces es afín; esta observación se desprende directamente de la definición de convexidad.
Véase también
 En inglés: Convex set Facts for Kids
En inglés: Convex set Facts for Kids
- Convexidad (economía)
- Concavidad
- Conjunto conexo
- Topología


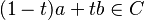
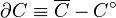
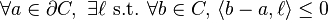
![\textbf{conv}(C) = \{t x + (1-t) y\,\,|\,\, x, y\in C,\, t\in [0;1]\}](/images/math/2/d/c/2dcbff98b257b32c4e233f36f2e95687.png)
![t \in [0;1]](/images/math/e/2/0/e20b3459f72a9c86fa17aeeed46a0767.png)