Epigrafo para niños
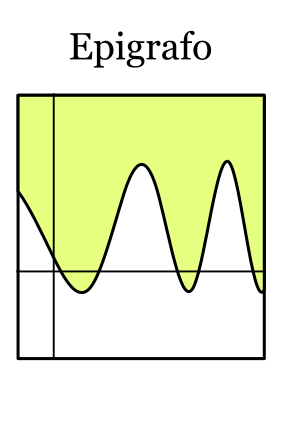
En matemática, el epígrafo de una función real es el conjunto de todos los puntos que se encuentran en la gráfica de la función o por encima de ella. Imagina que tienes una línea o una curva dibujada en un gráfico. El epígrafo sería toda la región que está por encima de esa línea, incluyendo la línea misma.
Por otro lado, el conjunto de puntos que están en la gráfica de la función o por debajo de ella se llama hipógrafo. Es como el "piso" de la función.
Contenido
¿Qué es un Epígrafo en Matemáticas?
Un epígrafo es una herramienta que usan los matemáticos para entender mejor las funciones. Piensa en una función como una regla que toma un número de entrada y te da un número de salida. Cuando dibujas esta función en un gráfico, obtienes una línea o una curva. El epígrafo es la colección de todos los puntos que están en esa línea o curva, y también todos los puntos que están justo encima de ella.
¿Cómo se ve un Epígrafo?
Si tienes una función simple, como una línea recta que sube, su epígrafo sería toda la región por encima de esa línea. Si la función es una curva que parece una "U" (como una parábola), el epígrafo sería toda la región dentro de la "U" y por encima de ella. Es como si la gráfica de la función fuera el borde inferior de una región infinita que se extiende hacia arriba.
¿Para qué sirve el Epígrafo?
Los epígrafos son muy útiles en áreas avanzadas de las matemáticas, especialmente en la optimización. Ayudan a los científicos y matemáticos a encontrar los mejores resultados posibles en problemas complejos. Por ejemplo, pueden usarse para encontrar el punto más bajo o más alto de una función, o para entender cómo se comportan las funciones en diferentes situaciones.
Epígrafo y Formas Especiales de Funciones
El epígrafo nos ayuda a identificar algunas características importantes de las funciones:
- Una función se llama convexa si su epígrafo es un conjunto convexo. Un conjunto convexo es como una forma que no tiene "huecos" o "curvas hacia adentro". Si tomas dos puntos dentro de un conjunto convexo y los unes con una línea recta, toda esa línea también estará dentro del conjunto. Las funciones convexas son importantes porque tienen una forma que se parece a un cuenco o una taza, lo que las hace más fáciles de analizar.
- Una función es inferiormente semicontinua si su epígrafo es un conjunto cerrado. Un conjunto cerrado incluye todos sus puntos "de borde". Esto significa que no hay "saltos" inesperados hacia abajo en la función.
Véase también
 En inglés: Epigraph (mathematics) Facts for Kids
En inglés: Epigraph (mathematics) Facts for Kids