Cardinalidad para niños
En matemáticas, la cardinalidad de un conjunto es una forma de medir cuántos elementos tiene. Es como decir el "tamaño" de un conjunto. Por ejemplo, si tienes un conjunto A = {2, 4, 6}, su cardinalidad es 3, porque tiene 3 elementos.
La cardinalidad de un conjunto A se escribe a menudo como | A |, usando dos líneas verticales. También se puede ver como n(A), A, card(A), o # A.
Contenido
¿Cómo se compara el tamaño de los conjuntos?
Para los conjuntos finitos (los que tienen un número limitado de elementos), la cardinalidad es simplemente contar sus elementos. Pero, ¿qué pasa con los conjuntos infinitos? Para ellos, necesitamos una forma especial de comparar sus tamaños.
Conjuntos con el mismo tamaño
Dos conjuntos A y B tienen la misma cardinalidad si puedes emparejar cada elemento de A con un elemento de B de forma única, sin que sobre ni falte ninguno en ninguno de los dos conjuntos. Esto se llama una biyección. Si esto ocurre, decimos que los conjuntos son "equipotentes".
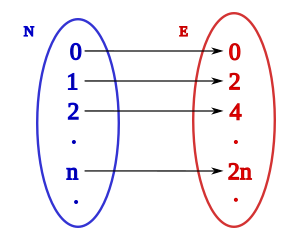
Por ejemplo, el conjunto E = {0, 2, 4, 6, ...} (los números pares no negativos) tiene el mismo tamaño que el conjunto N = {0, 1, 2, 3, ...} (los números naturales). Puedes emparejar cada número natural n con el número par 2n. Así, 0 va con 0, 1 con 2, 2 con 4, y así sucesivamente.
Conjuntos con tamaño menor o igual
Un conjunto A tiene una cardinalidad menor o igual que la de un conjunto B si puedes emparejar cada elemento de A con un elemento de B de forma única, sin que sobre ningún elemento en A. Puede que sobren elementos en B. Esto se llama una función inyectiva.
Conjuntos con tamaño estrictamente menor
Un conjunto A tiene una cardinalidad estrictamente menor que la de un conjunto B si puedes emparejar cada elemento de A con un elemento de B de forma única, pero no puedes emparejar todos los elementos de B con los de A. Es decir, siempre sobran elementos en B.
Por ejemplo, el conjunto N de los números naturales tiene una cardinalidad estrictamente menor que el conjunto R de los números reales. Aunque todos los números naturales son números reales, se ha demostrado que no puedes emparejar todos los números reales con los números naturales. Esto significa que hay "más" números reales que números naturales.
¿Qué son los números cardinales?
Los números cardinales son una forma de representar el "tamaño" de los conjuntos. Son como etiquetas que usamos para decir cuántos elementos tiene un conjunto.
Para los conjuntos finitos, los números cardinales son los números que ya conocemos: 0, 1, 2, 3, etc. Para los conjuntos infinitos, se usan símbolos especiales.
El número cardinal más pequeño para un conjunto infinito es álef-0 (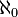
). Este es el tamaño del conjunto de los números naturales.
La cardinalidad de los números reales se llama "cardinalidad del continuo" y se escribe 
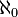. El matemático Georg Cantor demostró que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\mathfrak c} es mayor que . Esto significa que hay más números reales que números naturales.
Tipos de conjuntos según su tamaño
Si usamos una regla matemática llamada el "axioma de elección", podemos clasificar los conjuntos por su cardinalidad:
- Conjunto finito: Cualquier conjunto X que tiene una cardinalidad menor que la de los números naturales. Es decir, puedes contar sus elementos y llegar a un número.
- Conjunto infinito numerable: Cualquier conjunto X que tiene la misma cardinalidad que el conjunto de los números naturales. Aunque es infinito, puedes "contar" sus elementos uno por uno, como si los pusieras en una lista infinita. Su cardinalidad es .
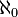- Conjunto no numerable: Cualquier conjunto X que tiene una cardinalidad mayor que la de los números naturales. No puedes "contar" sus elementos ni ponerlos en una lista infinita. El conjunto de los números reales es un ejemplo de conjunto no numerable.
Curiosidades de los conjuntos infinitos
Nuestra forma de pensar sobre el tamaño de los conjuntos cambia cuando hablamos de infinitos. A finales del siglo XIX, matemáticos como Georg Cantor descubrieron cosas sorprendentes. Por ejemplo, un conjunto infinito puede tener el mismo tamaño que una parte de sí mismo.
Un ejemplo famoso es la paradoja del hotel infinito de Hilbert. En este hotel, aunque todas las habitaciones estén ocupadas, siempre se puede hacer espacio para un nuevo huésped, ¡o incluso para un número infinito de huéspedes! Esto muestra que la intuición que tenemos con los números finitos no siempre funciona con los infinitos.
Cantor demostró que hay diferentes "tipos" de infinito, y algunos son más grandes que otros. El infinito más pequeño es el de los números naturales ().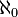
La cardinalidad del continuo
Cantor también descubrió que la cardinalidad de los números reales (
) es mayor que la de los números naturales (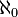). Esto significa que hay más puntos en una línea recta que números naturales.
Además, se ha demostrado que el número de puntos en una línea recta es igual al número de puntos en un plano, o incluso en cualquier espacio de dimensiones finitas. Esto parece muy extraño, porque un plano es mucho más grande que una línea. Sin embargo, matemáticamente, tienen el mismo "número" de puntos.
Cantor también demostró que existen conjuntos con una cardinalidad aún mayor que . Por ejemplo:
- El conjunto de todos los subconjuntos de los números reales.
- El conjunto de todas las funciones que van de los números reales a los números reales.
Ejemplos y propiedades de la cardinalidad
- Si X = {a, b, c} e Y = {manzanas, naranjas, peras}, entonces | X | = | Y | porque puedes emparejar cada elemento de X con uno de Y. La cardinalidad de ambos es 3.
- Si un conjunto X tiene una cardinalidad menor que un conjunto Y, entonces puedes encontrar una parte de Y que tenga el mismo tamaño que X.
- Si el conjunto X tiene una cardinalidad menor o igual que Y, y Y tiene una cardinalidad menor o igual que X, entonces X e Y tienen la misma cardinalidad. Esto es cierto incluso para conjuntos infinitos.
Unión e intersección de conjuntos
Cuando trabajamos con conjuntos, podemos combinarlos o encontrar sus elementos comunes.
- Si dos conjuntos A y B no tienen elementos en común (son disjuntos), entonces la cardinalidad de su unión (todos los elementos juntos) es la suma de sus cardinalidades:
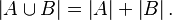
- En general, para cualquier par de conjuntos C y D, la suma de la cardinalidad de su unión y la cardinalidad de su intersección (elementos comunes) es igual a la suma de sus cardinalidades individuales:
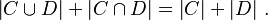
Véase también
