Cuerpo finito para niños
En matemáticas, un cuerpo finito (también conocido como campo finito o campo de Galois) es un sistema numérico. La característica principal de un cuerpo finito es que tiene un número limitado de elementos. Imagina un conjunto de números donde puedes sumar, restar, multiplicar y dividir (excepto por cero), y siempre obtienes un resultado que está dentro de ese mismo conjunto.
Cada cuerpo finito es único y se define por la cantidad de elementos que contiene. Esta cantidad siempre es una potencia de un número primo. Por ejemplo, puede tener 2, 3, 4, 5, 7, 8, 9, etc., elementos, pero nunca 6 o 10. El número primo base es muy importante para entender cómo funciona el cuerpo.
Contenido
Cuerpos Finitos: Un Mundo de Números Limitados
Los cuerpos finitos son como pequeños universos de números. A diferencia de los números que usamos normalmente (como los enteros o los números reales, que son infinitos), los cuerpos finitos tienen un número exacto y limitado de elementos. Esto los hace muy útiles en diferentes áreas de la ciencia y la tecnología.
¿Para qué sirven los Cuerpos Finitos?
Los cuerpos finitos son muy importantes en varias áreas de las matemáticas y la informática.
- Teoría de números: Ayudan a resolver problemas complejos relacionados con los números.
- Informática: Son fundamentales para la teoría de códigos. Por ejemplo, se usan para crear códigos que corrigen errores. Esto es lo que permite que un CD o DVD siga funcionando bien aunque tenga algunos arañazos.
- Criptografía: También se utilizan para crear sistemas de seguridad que protegen la información. Esto incluye los métodos que se usan para cifrar mensajes y mantenerlos secretos.
¿Quién descubrió los Cuerpos Finitos?
Aunque Carl Friedrich Gauss ya había investigado sobre ellos a finales del siglo XVIII, sus descubrimientos no se publicaron en su momento. Fue Évariste Galois quien, en 1830, publicó un trabajo donde los estudiaba a fondo. Por eso, a menudo se les llama "campos de Galois" en su honor.
El cuerpo finito con q elementos se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_q o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{GF}(q) . La letra "F" viene de "field" (campo en inglés) y "GF" de "Galois field".
Construyendo Cuerpos Finitos
Para construir un cuerpo finito, usamos un concepto llamado "congruencia". Esto es como la aritmética modular, donde los números "dan la vuelta" después de alcanzar un cierto valor.
El Cuerpo Finito Más Pequeño: F2
El cuerpo finito más pequeño se llama Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_2 . Solo tiene dos elementos: 0 y 1. En este cuerpo, las operaciones son un poco diferentes a las que conoces:
- Suma:
* 0 + 0 = 0 * 0 + 1 = 1 * 1 + 0 = 1 * 1 + 1 = 0 (¡sí, 1 más 1 es 0 en este cuerpo!)
- Multiplicación:
* 0 × 0 = 0 * 0 × 1 = 0 * 1 × 0 = 0 * 1 × 1 = 1
Este cuerpo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_2 es como el sistema binario que usan las computadoras. El 0 puede representar "falso" y el 1 "verdadero". La suma es como el "o exclusivo" y la multiplicación es como el "y" en lógica.
Cuerpos Finitos con Números Primos
Podemos construir cuerpos finitos con cualquier número primo p de elementos. Estos cuerpos se llaman Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_p . Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_3 tiene los elementos 0, 1 y 2. Las operaciones se hacen "módulo 3", lo que significa que después de sumar o multiplicar, tomas el resto de la división por 3.
Por ejemplo, en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_3 :
- 1 + 2 = 0 (porque 3 dividido por 3 da resto 0)
- 2 × 2 = 1 (porque 4 dividido por 3 da resto 1)
Un conjunto de números módulo p (donde p es un número primo) siempre forma un cuerpo finito.
Construyendo con Polinomios
Para construir cuerpos finitos con un número de elementos que sea una potencia de un primo (como 4, 8, 9, 16, etc.), usamos polinomios. Es un poco más complicado, pero la idea es similar a la de los números primos. Se toman polinomios y se hacen operaciones con ellos, pero "módulo" otro polinomio especial.
Por ejemplo, para construir un cuerpo con Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p^n elementos, necesitamos encontrar un polinomio especial de grado n que no se pueda "descomponer" en polinomios más pequeños.
Ejemplos de Cuerpos Finitos
Vamos a ver algunos ejemplos concretos de cómo funcionan estos cuerpos.
El Cuerpo Finito F7
El cuerpo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_7 tiene 7 elementos: [0], [1], [2], [3], [4], [5] y [6]. Las operaciones se hacen "módulo 7".
- Suma: [5] + [6] = [4] (porque 5 + 6 = 11, y 11 dividido por 7 da resto 4).
- Multiplicación: [5] × [6] = [2] (porque 5 × 6 = 30, y 30 dividido por 7 da resto 2).
En este cuerpo, cada elemento diferente de cero tiene un "inverso" para la multiplicación. Por ejemplo:
- [2] × [4] = [1] (porque 2 × 4 = 8, y 8 dividido por 7 da resto 1). Así, [4] es el inverso de [2].
El Cuerpo Finito F4
El cuerpo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_4 tiene 4 elementos. Se construye usando polinomios sobre Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_2 . Sus elementos son 0, 1, 
y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \alpha+1 . Aquí, es como un "número imaginario" especial que cumple la regla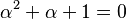 
.
Por ejemplo, para multiplicar por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \alpha+1 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (\alpha) (\alpha +1) = \alpha^2 + \alpha Como sabemos que 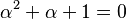, entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \alpha^2 + \alpha = 1 (porque en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_2 , 1 + 1 = 0, así que sumar 1 a ambos lados de la ecuación 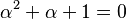nos da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \alpha^2 + \alpha = 1 ). Así, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (\alpha) (\alpha +1) = 1 .
Propiedades Interesantes
Los cuerpos finitos tienen algunas propiedades muy interesantes:
El Grupo Multiplicativo
Si tomas todos los elementos de un cuerpo finito (excepto el cero) y los multiplicas, forman un grupo especial llamado "grupo cíclico". Esto significa que hay un elemento "generador" que, al multiplicarlo por sí mismo varias veces, puede producir todos los demás elementos del grupo. Estos elementos generadores se llaman "elementos primitivos".
En la criptografía, es fácil calcular las potencias de un elemento primitivo, pero es muy difícil hacer lo contrario: encontrar qué potencia se usó para obtener un número dado. Esto se conoce como el "problema del logaritmo discreto" y es la base de muchos sistemas de seguridad.
Subcuerpos
Un cuerpo finito puede contener "subcuerpos", que son cuerpos finitos más pequeños dentro de él. Esto ocurre si el número de elementos del subcuerpo divide al número de elementos del cuerpo más grande. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_2 es un subcuerpo de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_4 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_8 .
Primeros Cuerpos Finitos en Tablas
Aquí puedes ver las tablas de suma y multiplicación para los primeros cuerpos finitos:
F2:
|
|
F3:
|
|
F4:
|
|
Nota: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{F}_4 = \mathbb{F}_2[\alpha] / \langle \alpha^2 + \alpha + 1\rangle
Véase también
En inglés: Galois field Facts for Kids
