Análisis de Fourier para niños
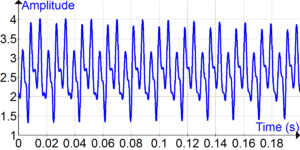
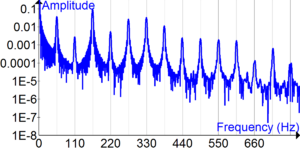
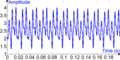
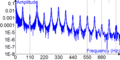
En el mundo de las matemáticas, el análisis de Fourier es una forma especial de estudiar cómo las cosas complejas pueden ser entendidas como la suma de partes más simples. Imagina que tienes una canción muy elaborada. El análisis de Fourier te ayuda a descubrir qué notas y sonidos individuales la componen.
Esta idea fue desarrollada por un matemático llamado Joseph Fourier. Él descubrió que si podías representar algo, como el calor que se mueve en un objeto, como una suma de ondas simples, era mucho más fácil de estudiar.
Hoy en día, el análisis de Fourier se usa en muchas áreas de las matemáticas y la ciencia. Cuando "descomponemos" algo en sus partes más simples, lo llamamos análisis de Fourier. Y cuando "reconstruimos" algo a partir de esas partes, lo llamamos síntesis de Fourier. Por ejemplo, para saber qué sonidos específicos forman una nota musical, se usa el análisis de Fourier. Luego, se podría volver a crear ese mismo sonido usando las partes que se encontraron.
La herramienta principal para esta descomposición se llama transformación de Fourier. El resultado de esta transformación se llama transformada de Fourier. Con el tiempo, esta idea se ha extendido a muchas otras áreas y ahora se conoce como análisis armónico. Cada transformación tiene una "transformación inversa" que nos permite volver a la forma original.
Contenido
¿Para qué sirve el análisis de Fourier?
El análisis de Fourier es muy útil en muchas áreas de la ciencia y la ingeniería. Aquí te mostramos algunos ejemplos:
- En la física, ayuda a entender cómo se mueven las ondas.
- En el procesamiento de señales, se usa para mejorar el sonido o las imágenes.
- En la teoría de la probabilidad y la estadística, ayuda a analizar datos.
- En la criptografía, se usa para proteger información.
- En la acústica, para estudiar el sonido.
- En la oceanografía, para entender las olas del mar.
- En la óptica, para trabajar con la luz.
Su gran utilidad se debe a varias propiedades importantes:
- Las transformadas son como "reglas" que se aplican de forma lineal, lo que significa que son fáciles de manejar.
- Casi siempre se pueden "deshacer", lo que permite reconstruir la información original.
- Ayudan a convertir problemas difíciles de ecuaciones diferenciales en problemas más sencillos de álgebra.
- Permiten que operaciones complicadas, como la convolución (que es como mezclar dos señales), se conviertan en multiplicaciones simples.
- La versión digital de la transformada de Fourier se puede calcular muy rápido con computadoras usando algoritmos especiales llamados FFT (Transformada Rápida de Fourier).
Usos en la vida diaria
El análisis de Fourier está presente en muchas cosas que usamos a diario:
- En la medicina forense, se usa para identificar materiales midiendo cómo absorben la luz infrarroja. Esto ayuda a los expertos a analizar pruebas.
- Cuando tomas una foto con tu cámara digital, la compresión JPEG usa una versión de la transformada de Fourier para hacer que el archivo de la imagen sea más pequeño. Así, puedes guardar más fotos en tu dispositivo.
¿Cómo se usa en el procesamiento de señales?
Cuando trabajamos con señales como el audio, las ondas de radio, las ondas de luz o las imágenes, el análisis de Fourier puede separar las partes más pequeñas de una señal compleja. Esto hace que sea más fácil detectar o eliminar ciertos componentes.
Algunos ejemplos incluyen:
- Mejorar el sonido de grabaciones de audio usando filtros.
- La forma en que tu teléfono celular recibe señales de radio digital.
- Mejorar imágenes para quitar imperfecciones o ruidos.
- En la cristalografía de rayos X, para entender la estructura de los materiales.
- En la espectroscopia, para analizar la composición de sustancias.
- Para crear espectrogramas que nos permiten ver cómo cambia el sonido con el tiempo.
- En el sonar pasivo, para identificar objetos bajo el agua por el ruido que hacen.
Historia del análisis de Fourier
Las ideas que llevaron al análisis de Fourier tienen raíces muy antiguas. Ya en las matemáticas babilónicas se usaban series armónicas para calcular las posiciones de los planetas. Los antiguos griegos también tenían conceptos relacionados en su forma de entender el movimiento de los cuerpos celestes.
En tiempos más recientes, matemáticos como Alexis Clairaut en 1754 y Joseph Louis Lagrange en 1759 usaron ideas similares para calcular órbitas y estudiar cuerdas que vibran.
Pero el gran avance llegó con Joseph Fourier en 1807. Él tuvo la idea revolucionaria de que casi cualquier función o patrón podía ser representado como una suma de ondas simples. Esta fue la base de lo que hoy conocemos como series de Fourier.
El desarrollo de este campo se conoce como análisis armónico. El primer algoritmo para la transformada rápida de Fourier (FFT), que permite hacer estos cálculos muy rápido, fue descubierto por Carl Friedrich Gauss alrededor de 1805, aunque se hizo más conocido gracias a otros investigadores más tarde.
Transformaciones de tiempo-frecuencia
Imagina que una señal tiene dos características importantes: el tiempo (cuándo ocurre algo) y la frecuencia (qué tan rápido se repite). La transformada de Fourier nos da mucha información sobre la frecuencia, pero no tanto sobre el tiempo.
Para tener información de ambos, se usan otras herramientas llamadas transformadas de tiempo-frecuencia. Estas son como versiones más avanzadas de la transformada de Fourier. Algunas de ellas son la Transformada de Fourier de Tiempo Reducido o las transformadas de ondícula. Estas herramientas nos ayudan a entender mejor cómo cambian las señales a lo largo del tiempo y en diferentes frecuencias.
Galería de imágenes
Véase también
 En inglés: Fourier analysis Facts for Kids
En inglés: Fourier analysis Facts for Kids