Vector unitario para niños
En álgebra lineal y física, un vector unitario o versor es un vector de módulo uno. En ocasiones se le llama también vector normalizado.
Contenido
Notación
Un vector unitario se denota frecuentemente con un acento circunflejo sobre su nombre, como 
(se lee "r vector" o "vector r"). La notación mediante el uso de una breve (
) también es común, especialmente en desarrollos manuscritos. La tendencia actual es representar el vector en la dirección del vector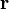 
en la forma 
.
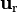Definición formal
- Sea el vector v ∈ ℝn. Se dice que v es un vector unitario y se denota mediante
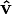si y sólo si el módulo de v es igual a 1.
O en forma más compacta:
Versor asociado a un vector
Con frecuencia resulta conveniente disponer de un vector unitario que tenga la misma dirección que un vector dado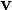 
. A tal vector se le llama versor asociado al vector 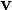y se puede representar bien sea 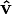por o por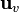 
e indica una dirección en el espacio.
La operación que permite hallar 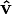es la división del vector entre su módulo.
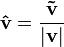
Al proceso de obtener un versor asociado a un vector se le conoce como normalización del vector, razón por la cual es común referirse a un vector unitario como vector normalizado.
El método para transformar una base ortogonal (obtenida, por ejemplo mediante el método de ortogonalización de Gram-Schmidt) en una base ortonormal (es decir, una base en la que todos los vectores son versores) consiste simplemente en normalizar todos los vectores de la base utilizando la ecuación anterior.
Producto escalar de dos vectores
En el espacio euclídeo, el producto escalar de dos vectores unitarios es simplemente el coseno del ángulo entre ellos. Esto es consecuencia de la definición de producto escalar y del hecho de que el módulo de ambos vectores es la unidad:
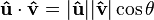
Pero:
Por lo tanto:
donde θ es el ángulo entre ambos vectores.
Proyección escalar
De lo anterior, resulta que el producto de un vector por un versor (o vector unitario) es la proyección escalar del vector sobre la dirección determinada por el vector.
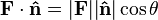
Como el módulo del vector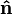 
es la unidad, la ecuación anterior se transforma en:
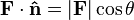
de donde es evidente lo afirmado al comienzo de este apartado. Este resultado es muy frecuente en física, donde en necesario operar, por ejemplo, con las componentes ortogonales a una superficie.
Versores cartesianos
Los versores asociados con las direcciones de los ejes coordenados cartesianos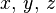 
se designan por 
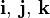, respectivamente. Los versores cartesianos permiten expresar analíticamente los vectores por medio de sus componentes cartesianas. Ejemplo: la expresión analítica del vector 
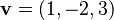es
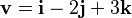
Véase también
En inglés: Unit vector Facts for Kids
- Vector
- Base ortonormal
- Coordenadas
- Coordenadas cartesianas
- Coordenadas polares
- Coordenadas curvilíneas
- Módulo
