Conjugado (matemática) para niños
En matemáticas, el conjugado de un número complejo es un concepto importante. Se obtiene cambiando el signo de la parte imaginaria de ese número.
Imagina un número complejo como este:
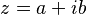
Aquí, a es la parte real y b es la parte imaginaria, y i es la unidad imaginaria (que cumple 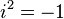 ).
).
El conjugado de este número se escribe así:
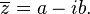
A veces, el conjugado también se indica como 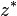 . En este artículo, usaremos
. En este artículo, usaremos 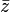 para que no se confunda con otras notaciones.
para que no se confunda con otras notaciones.
Por ejemplo:
- El conjugado de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3-2i es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3+2i .
- El conjugado de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7i es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -7i .
- El conjugado de
 es
es 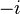 .
.
Contenido
¿Cómo se ve el conjugado en un plano?
Los números complejos se pueden dibujar como puntos en un plano complejo. Este plano es como un sistema de coordenadas cartesianas. El eje horizontal (eje x) representa los números reales, y el eje vertical (eje y) representa los múltiplos de i (la unidad imaginaria).
Cuando dibujas un número complejo y su conjugado, verás que el conjugado es como un reflejo del número original sobre el eje x. Es decir, si doblas el plano por el eje x, el número y su conjugado coincidirían.
Si un número complejo está en su forma polar, que es 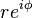 , su conjugado es
, su conjugado es 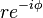 . Esto se puede entender usando la fórmula de Euler.
. Esto se puede entender usando la fórmula de Euler.
Los pares de números y sus conjugados son muy útiles. Por ejemplo, si un número complejo es la solución de un problema matemático, es muy común que su conjugado también lo sea. Esto ocurre, por ejemplo, con las soluciones complejas de la ecuación de segundo grado cuando los números que la forman son reales.
Propiedades del conjugado de un número complejo
Estas son algunas reglas importantes que se cumplen para cualquier número complejo 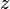 y
y 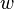 :
:
- Suma: El conjugado de una suma es la suma de los conjugados.
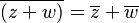
- Resta: El conjugado de una resta es la resta de los conjugados.
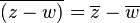
- Multiplicación: El conjugado de un producto es el producto de los conjugados.
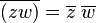
- División: El conjugado de una división es la división de los conjugados (siempre que el número de abajo no sea cero).
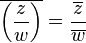
- Números reales: Un número es igual a su conjugado si y solo si es un número real.
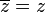
- Potencias: El conjugado de un número elevado a una potencia es igual al conjugado del número elevado a esa misma potencia.

- Módulo (tamaño): Un número complejo y su conjugado tienen el mismo módulo (o "tamaño").
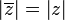
- Producto con su conjugado: El producto de un número por su conjugado es igual al módulo del número al cuadrado.
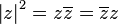
- Inverso: Para encontrar el inverso de un número complejo (si no es cero), puedes usar esta fórmula:
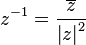
- Producto de partes: Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z=a+ib , entonces
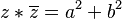 , que siempre es diferente de cero si
, que siempre es diferente de cero si 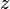 no es cero.
no es cero. - Simetría: Geométricamente, el conjugado de un número complejo es un vector simétrico (reflejado) del número original, respecto al eje horizontal (eje OX).
- Derivadas: El conjugado de la derivada de un número complejo es igual a la derivada de su conjugado.
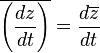
Conjugado de un hipercomplejo
La idea de número conjugado también se puede aplicar a otros tipos de números más complejos, llamados números hipercomplejos. Por ejemplo, para un cuaternión (un tipo de número hipercomplejo), el conjugado se obtiene cambiando el signo de sus partes imaginarias:

Las propiedades que vimos para los números complejos también se cumplen para los conjugados de los números hipercomplejos.
Aplicaciones del conjugado
El conjugado de un número complejo es muy útil en varias situaciones:
- Simplificar divisiones: Ayuda a dividir números complejos. Al multiplicar el numerador y el denominador por el conjugado del denominador, se logra que el denominador se convierta en un número real, lo que facilita la operación. Es similar a la "racionalización" que se hace con las raíces cuadradas.
- Calcular el módulo: Permite calcular el módulo (o "tamaño") de cualquier número complejo de forma sencilla.
Véase también
 En inglés: Complex plane Facts for Kids
En inglés: Complex plane Facts for Kids


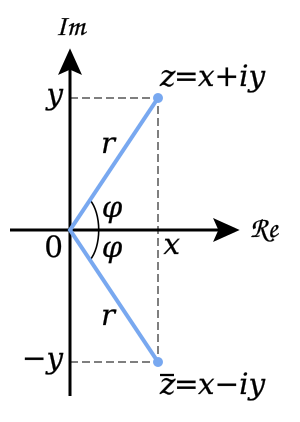
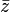 en el plano complejo.
en el plano complejo.