Teorema de la inversión de Fourier para niños
El teorema de la inversión de Fourier es una idea importante en las matemáticas que nos ayuda a entender cómo funcionan las ondas y las señales. Imagina que tienes una canción. Esa canción está hecha de muchas notas musicales diferentes, cada una con su propio tono (frecuencia) y su momento exacto (fase).
Este teorema dice que si conoces todas las "piezas" de una señal, como todas las frecuencias y sus fases, entonces puedes reconstruir la señal original de forma perfecta. Es como si pudieras desarmar un juguete en todas sus piezas y luego, con esas mismas piezas, volver a armar el juguete exactamente como era antes.
En matemáticas, esto se aplica a las funciones. Una función es como una regla que nos dice cómo se relaciona una cosa con otra. La transformada de Fourier toma una función y la convierte en otra función que nos muestra sus componentes de frecuencia. El teorema de la inversión de Fourier nos dice cómo usar esa información de frecuencia para volver a la función original.
Contenido
¿Qué es la Transformada de Fourier?
Para entender el teorema, primero necesitamos saber qué es la transformada de Fourier. Piensa en ella como una herramienta mágica que toma una señal compleja (como una grabación de voz o una imagen) y la descompone en sus partes más simples.
Por ejemplo, si tienes una grabación de música, la transformada de Fourier puede decirte qué tan fuerte es cada nota (frecuencia) en cada momento. Es como si te diera la "receta" completa de la señal, mostrando todos sus ingredientes básicos.
¿Qué nos dice el Teorema de Inversión de Fourier?
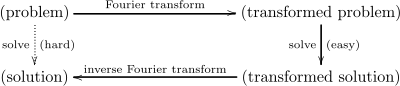
El teorema de la inversión de Fourier es la "receta inversa". Si ya tienes la información de la transformada de Fourier (es decir, la "receta" de las frecuencias y fases), este teorema te da las instrucciones para volver a construir la señal original.
En términos matemáticos, si tienes una función f y calculas su transformada de Fourier (que a veces se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{F}f ), el teorema dice que puedes usar una fórmula especial para obtener f de nuevo a partir de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{F}f .
Esto es muy útil porque a veces es más fácil trabajar con las "piezas" de una señal (sus frecuencias) que con la señal completa.
¿Para qué sirve este Teorema?
El teorema de la inversión de Fourier es muy importante en muchas áreas de la ciencia y la ingeniería.
Resolver Problemas Complejos
En muchos problemas, especialmente los relacionados con las ecuaciones diferenciales (que describen cómo cambian las cosas con el tiempo o el espacio), es más fácil resolverlos si primero los transformamos usando la transformada de Fourier. Una vez que el problema transformado se resuelve, el teorema de la inversión de Fourier nos permite volver a la solución del problema original.
Procesamiento de Señales
Este teorema es fundamental en el procesamiento de señales. Por ejemplo, cuando escuchas música en tu teléfono o ves una película, se utilizan transformadas de Fourier para comprimir los datos y luego el teorema de inversión para reconstruir el sonido o la imagen. También se usa en:
- Comunicaciones: Para enviar y recibir señales de radio o televisión.
- Imágenes médicas: Como en las resonancias magnéticas, donde se recogen datos de frecuencia y luego se reconstruye la imagen del cuerpo.
- Análisis de sonido: Para entender las diferentes frecuencias en la voz humana o en instrumentos musicales.
Relación con las Series de Fourier
El teorema de la inversión de Fourier es como una versión más avanzada de las series de Fourier. Las series de Fourier se usan para descomponer señales que se repiten (como una onda de sonido constante) en una suma de ondas simples. El teorema de la inversión de Fourier hace algo similar, pero para señales que no se repiten y que pueden extenderse infinitamente.
En ambos casos, la idea principal es la misma: descomponer algo complejo en sus partes más simples (frecuencias) y luego poder volver a armarlo.
Propiedades de la Transformada Inversa
La transformada de Fourier inversa es muy parecida a la transformada de Fourier original. La principal diferencia es una pequeña modificación en la fórmula. Debido a esta similitud, muchas de las propiedades que tiene la transformada de Fourier también las tiene su inversa. Esto hace que sea muy práctico trabajar con ellas en diferentes aplicaciones.
Véase también
 En inglés: Fourier inversion theorem Facts for Kids
En inglés: Fourier inversion theorem Facts for Kids