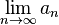robot de la enciclopedia para niños

Límite de una sucesión para niños

Enciclopedia para niños

El límite de una sucesión es un concepto muy importante en las matemáticas. Imagina que tienes una lista de números que siguen un patrón, como 16, 8, 4, 2, 1, 0.5, y así sucesivamente, donde cada número es la mitad del anterior. Si sigues esta lista infinitamente, los números se acercan cada vez más a un valor específico. Ese valor al que se acercan es el límite de la sucesión.

En el ejemplo de 16, 8, 4, ..., los números se acercan cada vez más a cero. Entonces, decimos que el límite de esa sucesión es 0.

Se representa así:

\lim_{n\to\infty} a_n

Esto se lee "límite cuando n tiende a infinito de a sub n". Significa que estamos viendo qué pasa con los números de la sucesión (llamados a sub n) cuando n (la posición del número en la lista) se hace muy, muy grande.

Este concepto está muy relacionado con la idea de convergencia. Una sucesión es convergente si sus números se acercan a un valor específico. Ese valor es su límite. Si una sucesión tiene un límite, decimos que "converge" o "tiende" a ese límite. Si los números de la sucesión no se acercan a un valor fijo, entonces la sucesión es divergente.

La idea principal es que, si una sucesión tiene un límite, todos sus números, a partir de cierto punto, estarán tan cerca del límite como queramos.

Archivo:Sucesión 001
Representación gráfica de la sucesión: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_0 = 16; a_{n+1} = \frac{a_n}{2}
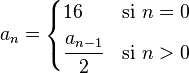a_{n} = \begin{cases} 16 & \mbox{si } n = 0 \\ \cfrac{a_{n-1}}{2} & \mbox{si } n > 0 \end{cases}
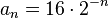a_{n} = 16 \cdot 2^{-n}

Límite de una Sucesión: ¿Qué es y por qué es importante?

El límite de una sucesión es el valor al que se acercan los términos de una lista ordenada de números a medida que avanzamos en esa lista. Es como el destino final de un viaje que nunca termina.

¿Qué es una Sucesión Matemática?

Una sucesión matemática es una lista de números que siguen un orden específico. Cada número en la lista se llama "término" y tiene una posición (primero, segundo, tercero, etc.). Por ejemplo, en la sucesión 2, 4, 6, 8, ..., el primer término es 2, el segundo es 4, y así.

¿Qué significa que una Sucesión "Converja"?

Cuando una sucesión converge, significa que sus términos se van acercando cada vez más a un número fijo. Este número fijo es el límite. Piensa en una flecha que se acerca a un blanco: cuanto más cerca está, más "converge" a ese blanco.

Ejemplos Sencillos de Sucesiones Convergentes

Aquí tienes algunos ejemplos para entenderlo mejor:

  • La sucesión 1/1, 1/2, 1/3, 1/4, ... (es decir, 1, 0.5, 0.333..., 0.25, ...) se acerca al número 0. Su límite es 0.
  • La sucesión 1/2, 3/4, 7/8, 15/16, ... (que se forma sumando 1/2 + 1/4, luego 1/2 + 1/4 + 1/8, etc.) se acerca al número 1. Su límite es 1.
  • Si tienes un número a entre -1 y 1 (sin incluir -1 y 1), la sucesión a elevado a n (an) tiene un límite de 0. Por ejemplo, si a es 0.5, la sucesión 0.5, 0.25, 0.125, ... se acerca a 0.

¿Cuándo una Sucesión no tiene Límite? (Divergencia)

Si una sucesión no se acerca a un único valor fijo, decimos que es divergente.

  • La sucesión 1, -1, 1, -1, 1, ... es un ejemplo. Sus términos saltan entre 1 y -1, nunca se acercan a un solo número. Se le llama oscilante.
  • La sucesión 1, 2, 3, 4, ... (los números naturales) también es divergente, porque sus términos crecen sin parar y no se acercan a ningún número fijo.

Propiedades Clave de las Sucesiones Convergentes

Las sucesiones que convergen tienen algunas características interesantes:

Límite Único y Signo de los Términos

  • Si una sucesión converge, siempre lo hace a un único valor. No puede tener dos límites diferentes.
  • Si el límite de una sucesión es un número positivo, entonces, a partir de cierto punto, todos los términos de la sucesión también serán positivos.
  • De manera similar, si el límite es negativo, a partir de cierto punto, todos los términos serán negativos.

Sucesiones Acotadas y Operaciones con Límites

  • Si una sucesión tiene un límite, significa que sus términos no crecen infinitamente ni se hacen infinitamente pequeños. Siempre hay un número máximo y un número mínimo que los términos no superan. Decimos que la sucesión está "acotada".
  • Si sumas, restas, multiplicas o divides dos sucesiones que tienen límite (y en el caso de la división, el límite de la segunda no es cero), el resultado también será una sucesión con límite. Y ese límite será la suma, resta, producto o división de los límites originales.
  • Una regla muy útil es que si una sucesión es "monótona" (siempre crece o siempre decrece) y está "acotada" (sus valores no se van al infinito), entonces ¡siempre converge!

Tipos de Convergencia en Funciones: Puntual y Uniforme

Cuando hablamos de sucesiones de funciones (listas de funciones en lugar de números), hay diferentes maneras en que pueden converger.

Convergencia Puntual: Un Punto a la Vez

La convergencia puntual significa que, si tomas un punto específico, las funciones de la sucesión se acercan al valor de la función límite en ese punto. Es como si cada punto de la función tuviera su propia sucesión de números que converge.

Convergencia Uniforme: Todos los Puntos a la Vez

La convergencia uniforme es una forma más "fuerte" de convergencia. Significa que las funciones de la sucesión se acercan a la función límite de manera "pareja" en todos los puntos al mismo tiempo. Es como si toda la gráfica de la función se acercara a la gráfica de la función límite. Si una sucesión de funciones converge uniformemente, también converge puntualmente.

Sucesiones en otros espacios matemáticos

El concepto de límite no solo se aplica a números, sino también a elementos en otros tipos de "espacios" matemáticos, donde podemos medir distancias. La idea es la misma: los elementos de la sucesión se acercan cada vez más a un punto específico en ese espacio.

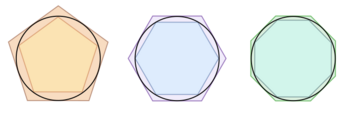
Archivo:Archimedes pi
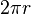Diagrama de un hexágono y un pentágono circunscritos fuera de un círculo. La sucesión dada por los perímetros de polígonos regulares de n lados que circunscriben el círculo unitario tiene un límite igual al perímetro del círculo, es decir, 2\pi r. La sucesión correspondiente para polígonos inscritos tiene el mismo límite.

La Historia del Límite: Desde la Antigua Grecia hasta Hoy

La idea de límite no es nueva.

  • El filósofo griego Zenón de Elea (hace más de 2000 años) ya planteaba paradojas que implicaban procesos de acercamiento infinito.
  • Matemáticos como Arquímedes usaron el "método de agotamiento" para calcular áreas y volúmenes, acercándose cada vez más a la forma deseada con una secuencia infinita de figuras.
  • En el siglo XVII, matemáticos como Grégoire de Saint-Vincent y Pietro Mengoli empezaron a definir el límite de una serie geométrica, diciendo que era el valor al que la serie se podía acercar "más que un segmento dado".
  • Isaac Newton también trabajó con series infinitas en sus estudios.
  • En el siglo XVIII, matemáticos como Leonhard Euler usaban límites, aunque no siempre con el rigor que tenemos hoy.
  • Fue en el siglo XIX cuando matemáticos como Bernard Bolzano y Karl Weierstrass dieron la definición moderna y rigurosa de límite que usamos hoy en día, usando la idea de que "para cualquier distancia pequeña que elijas, los términos de la sucesión estarán dentro de esa distancia del límite a partir de cierto punto".

Véase también

Kids robot.svg En inglés: Limit of a sequence Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Límite_de_una_sucesión&oldid=5065383»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Límite de una sucesión para Niños. Enciclopedia Kiddle.