Problema del caballo para niños
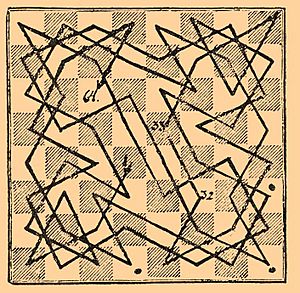
El problema del caballo es un desafío matemático muy antiguo que se basa en el juego del ajedrez. Imagina un tablero de ajedrez de cualquier tamaño, por ejemplo, uno de 8x8 casillas como los que usamos normalmente. El reto consiste en colocar un caballo de ajedrez en una casilla y moverlo de tal manera que visite cada una de las casillas del tablero exactamente una vez.
Contenido
¿Quién ha estudiado el problema del caballo?
Muchos matemáticos famosos han intentado resolver este problema a lo largo de la historia. Uno de ellos fue Leonhard Euler, un matemático muy importante del siglo XVIII. Él y otros han encontrado muchas maneras de resolverlo, pero aún no se sabe con exactitud cuántas soluciones diferentes existen en total.
Variaciones del desafío
El problema del caballo tiene algunas variaciones interesantes que los matemáticos también han explorado:
- Soluciones cíclicas: En este caso, el caballo debe terminar su recorrido en una casilla desde la cual pueda saltar directamente a la casilla donde empezó. Es como cerrar un círculo.
- Tableros diferentes: Se puede intentar resolver el problema en tableros de ajedrez que no sean cuadrados, por ejemplo, con más columnas que filas, o viceversa.
- Juegos basados en la idea: Se han creado juegos para dos jugadores que usan la misma idea de mover el caballo por el tablero.
- Movimientos especiales: A veces, se cambia un poco la forma en que el caballo se mueve para ver cómo afecta al problema.
Este problema es un ejemplo de un desafío más grande en las matemáticas llamado el problema de la ruta Hamiltoniana. Este problema se estudia en una rama de las matemáticas conocida como la teoría de grafos, que analiza cómo se conectan diferentes puntos o elementos.
Ejemplos de soluciones
En un tablero de ajedrez normal de 8x8, hay muchas soluciones posibles. Una de ellas se muestra en la imagen animada, donde el caballo realiza 63 saltos para visitar las 64 casillas. También se han encontrado soluciones cíclicas, donde el último salto del caballo lo lleva a una casilla desde la que puede volver a la casilla inicial.
El problema del caballo en la literatura
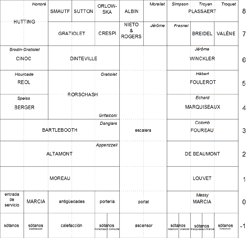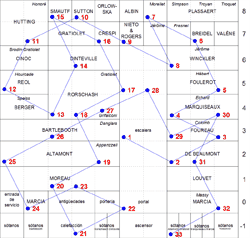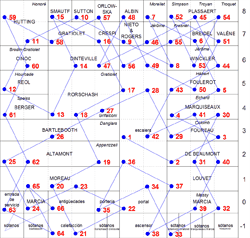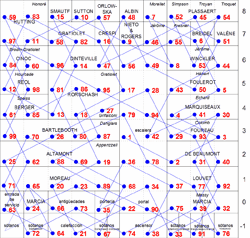
El problema del caballo ha inspirado incluso a escritores. Por ejemplo, en la novela La vida instrucciones de uso (1978) del autor Georges Perec, los capítulos están organizados siguiendo una solución del problema del caballo en un tablero imaginario de 10x10. El propio autor encontró esta solución probando diferentes caminos.
Véase también
 En inglés: Knight's tour Facts for Kids
En inglés: Knight's tour Facts for Kids