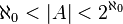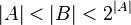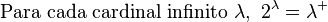Hipótesis del continuo para niños

La hipótesis del continuo es una idea importante en las matemáticas, especialmente en una rama llamada teoría de conjuntos. Fue propuesta por el matemático Georg Cantor en 1878.

Esta hipótesis se pregunta sobre el "tamaño" de los conjuntos infinitos. Imagina que tienes el conjunto de los números naturales (1, 2, 3, ...), que es infinito. Luego, tienes el conjunto de los números reales, que incluye todos los números que puedes encontrar en una línea, como 1, 2.5, pi (π), etc. Este conjunto también es infinito, pero es "más grande" que el de los números naturales.

La hipótesis del continuo dice que no existe ningún conjunto infinito cuyo tamaño sea intermedio entre el de los números naturales y el de los números reales. Es decir, no hay un infinito "entre" estos dos.

Esta hipótesis fue uno de los 23 problemas más importantes que el matemático David Hilbert propuso en el año 1900. Más tarde, los matemáticos Kurt Gödel y Paul Cohen demostraron que esta hipótesis es "independiente" de las reglas básicas de la teoría de conjuntos (llamadas axiomas de Zermelo-Fraenkel). Esto significa que no se puede probar si es verdadera o falsa usando solo esas reglas.

¿Qué son los tamaños de los conjuntos infinitos?

En la teoría de conjuntos, usamos algo llamado "número cardinal" para medir el tamaño de los conjuntos, incluso los infinitos.

• El tamaño del conjunto de los números naturales (que se escribe como N) se llama álf-cero (ℵ₀). Los conjuntos que tienen este mismo tamaño, como los números enteros (..., -1, 0, 1, ...) o los números racionales (fracciones), se llaman numerables.
• El conjunto de los números reales (que se escribe como R) tiene un tamaño más grande. A este tamaño se le llama c (por "continuo"). Este tamaño es igual a 2^ℵ₀.

Para entender por qué el tamaño de los números reales es 2^ℵ₀, piensa en cuántas combinaciones puedes hacer. Si tienes un número con 3 cifras, hay 10³ (1000) valores posibles. Un número real puede tener una cantidad infinita de cifras después del punto decimal. La cantidad de números reales es como la cantidad de subconjuntos que se pueden formar con los números naturales.

Un subconjunto infinito de los números reales puede tener el tamaño de los números naturales (ℵ₀), o el tamaño de los números reales (2^ℵ₀}). La hipótesis del continuo afirma que no es posible encontrar un subconjunto de los números reales que tenga un tamaño entre ℵ₀ y 2^ℵ₀}.

La hipótesis del continuo explicada

La hipótesis del continuo dice que no hay conjuntos con tamaños infinitos intermedios entre los números naturales y los números reales.

Si aceptamos una regla matemática llamada el axioma de elección, entonces los tamaños infinitos se pueden ordenar de forma clara. Después de ℵ₀, el siguiente tamaño infinito más grande se llama ℵ₁ (álf-uno). En este caso, la hipótesis del continuo es lo mismo que decir:

Historia y su independencia

Georg Cantor, quien propuso esta hipótesis, creía que era verdadera e intentó demostrarla, pero no lo logró. El problema se hizo tan famoso que David Hilbert lo incluyó como el primero de sus 23 problemas matemáticos más importantes del siglo XX.

Sin embargo, la hipótesis del continuo es "independiente" o "indecidible". Esto significa que, usando las reglas básicas de la teoría de conjuntos (los axiomas de Zermelo-Fraenkel), no se puede probar si es verdadera ni si es falsa.

• En 1940, Kurt Gödel demostró que la hipótesis del continuo no puede ser falsa si las reglas de la teoría de conjuntos son consistentes.
• En 1963, Paul Cohen demostró que la hipótesis del continuo no puede ser verdadera usando esas mismas reglas.

Estos descubrimientos mostraron que la hipótesis del continuo es un problema único en las matemáticas, ya que su verdad o falsedad no se puede determinar solo con los axiomas estándar.

Diferentes puntos de vista

A lo largo de la historia, los matemáticos han tenido diferentes opiniones sobre si la hipótesis del continuo debería ser verdadera o falsa.

Algunos matemáticos, como Gödel, pensaban que la hipótesis del continuo era falsa. Creían que el universo de los conjuntos es mucho más "rico" y "grande" de lo que la hipótesis sugiere. Otros, en cambio, preferían un universo de conjuntos más "ordenado" y "controlable", y por eso apoyaban la hipótesis.

También existe la idea de que la forma en que entendemos el concepto de "conjunto" no es lo suficientemente precisa como para decidir si la hipótesis del continuo es verdadera o falsa. Algunos matemáticos creen que necesitamos nuevas reglas o axiomas para poder resolverla.

Por ejemplo, el matemático William Hugh Woodin ha propuesto argumentos complejos que sugieren que la hipótesis del continuo es falsa. Sin embargo, más recientemente, ha cambiado de opinión y ahora cree que podría ser verdadera, basándose en nuevas ideas.

Otros matemáticos, como Solomon Feferman, han argumentado que la hipótesis del continuo no es un problema matemático "definido" en el sentido tradicional, y que quizás no tenga un valor de verdad claro (ni verdadero ni falso).

También hay un enfoque que sugiere que la teoría de conjuntos tiene muchos "universos" posibles. Desde esta perspectiva, la hipótesis del continuo podría ser verdadera en algunos de esos universos y falsa en otros, lo que significa que no hay una única respuesta definitiva.

Hipótesis del continuo generalizada

La hipótesis del continuo también tiene una versión más amplia, llamada hipótesis del continuo generalizada.

Recuerda que el conjunto de los números reales tiene el mismo tamaño que el conjunto de todos los subconjuntos posibles de los números naturales. La hipótesis del continuo generalizada extiende esta idea a cualquier conjunto infinito.

Aquí, 2^|A| representa el tamaño del conjunto de todos los subconjuntos de A.

Si se asume el axioma de elección, la hipótesis del continuo generalizada se puede expresar de forma más sencilla:

Al igual que la hipótesis del continuo original, la hipótesis del continuo generalizada también es independiente de los axiomas estándar de la teoría de conjuntos. De hecho, es tan poderosa que si fuera verdadera, implicaría que el axioma de elección también es verdadero.

Galería de imágenes

• Georg Cantor.jpg

  Georg Cantor, el matemático que propuso la hipótesis del continuo.

• Kurt Gödel.jpg

  Kurt Gödel demostró que la hipótesis del continuo no se puede refutar.

• Paul Cohen.jpg

  Paul Cohen demostró que la hipótesis del continuo no se puede probar.

Véase también

En inglés: Continuum hypothesis Facts for Kids