Pierre Fatou para niños
Datos para niños Pierre Fatou |
||
|---|---|---|
 |
||
| Información personal | ||
| Nacimiento | 28 de febrero de 1878 Lorient (Francia) |
|
| Fallecimiento | 9 de agosto de 1929 Pornichet (Francia) |
|
| Sepultura | Cimetière de Carnel | |
| Nacionalidad | Francesa | |
| Familia | ||
| Padre | Ernest Fatou | |
| Educación | ||
| Educado en |
|
|
| Supervisor doctoral | Paul Painlevé | |
| Información profesional | ||
| Ocupación | Matemático, astrónomo y profesor universitario | |
| Área | Dinámica holomorfa, matemáticas, análisis matemático, astronomía y mecánica celeste | |
| Empleador | Observatorio de París | |
| Distinciones |
|
|
Pierre Joseph Louis Fatou fue un importante matemático y astrónomo francés. Nació en Lorient, Francia, el 28 de febrero de 1878 y falleció el 9 de agosto de 1929 en Pornichet. Es conocido por sus estudios en un área de las matemáticas llamada dinámica compleja.
Contenido
¿Quién fue Pierre Fatou?
Pierre Fatou fue un científico que dedicó su vida a entender cómo funcionan los números y el universo. Sus descubrimientos ayudaron a otros matemáticos a explorar patrones complejos.
Sus primeros años y estudios
Desde joven, Pierre Fatou mostró un gran interés por las matemáticas. En 1898, ingresó a la École Normale Supérieure de París, una de las escuelas más prestigiosas de Francia. Allí, se especializó en matemáticas y se graduó en 1901.
Un astrónomo y matemático
Después de terminar sus estudios, Pierre Fatou consiguió un trabajo como astrónomo en el Observatorio de París. Esto le permitió combinar su amor por las matemáticas con su interés en el espacio y los cuerpos celestes.
¿Qué son los números complejos?
Para entender el trabajo de Fatou, es útil saber qué son los números complejos. Son un tipo de número que tiene dos partes: una parte "real" y una parte "imaginaria". Se usan mucho en matemáticas, física e ingeniería.
El fascinante mundo de la dinámica compleja
Pierre Fatou se dedicó a estudiar algo llamado "procesos iterativos". Imagina que tienes una fórmula matemática y repites esa fórmula una y otra vez, usando el resultado anterior como el nuevo punto de partida. Fatou estudió cómo se comportaban estos procesos, especialmente cuando se usaban números complejos.
Por ejemplo, analizó la fórmula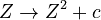 
, donde Z y c son números complejos. Quería saber qué pasaba con los resultados a medida que repetía la operación.
La conexión con el conjunto de Mandelbrot
El trabajo de Fatou fue muy avanzado para su época. Años después, en el XX, otro matemático llamado Benoît Mandelbrot retomó estas ideas. Usando computadoras, Mandelbrot pudo visualizar los patrones que surgían de las fórmulas de Fatou.
Así fue como se creó la famosa imagen del conjunto de Mandelbrot. Este conjunto es una representación gráfica de cómo se comportan las series de números complejos que Fatou había estudiado. Es un ejemplo hermoso de cómo las matemáticas pueden crear arte.
Véase también
En inglés: Pierre Fatou Facts for Kids
