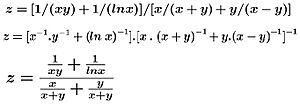Orden de evaluación para niños
La prioridad de las operaciones es un conjunto de reglas que nos dice en qué orden debemos resolver los cálculos en una expresión matemática. Imagina que tienes una receta con varios pasos: si no sigues el orden correcto, el resultado no será el esperado. En matemáticas, estas reglas aseguran que todos obtengamos el mismo resultado al resolver un problema.
Es muy importante conocer estas reglas para usar calculadoras o programas de computadora, ya que ellos también siguen este orden para darte la respuesta correcta.
Las reglas principales son:
- Primero, resuelve lo que está dentro de los paréntesis, corchetes o llaves. También, las líneas de fracción o los símbolos de raíz cuadrada actúan como paréntesis, agrupando lo que está debajo o dentro de ellos.
- Segundo, calcula las potencias y las raíces.
- Tercero, haz las multiplicaciones y divisiones.
- Cuarto, realiza las sumas y restas.
Cuando tienes operaciones del mismo nivel (por ejemplo, varias multiplicaciones y divisiones, o varias sumas y restas), generalmente se resuelven de izquierda a derecha.
Por ejemplo, en la expresión 2 + 3 × 4: Si sumaras primero (2 + 3 = 5) y luego multiplicaras (5 × 4 = 20), el resultado sería incorrecto. Siguiendo la prioridad, primero multiplicamos (3 × 4 = 12) y luego sumamos (2 + 12 = 14). El resultado correcto es 14.
Los paréntesis son muy útiles para cambiar el orden si lo necesitas. Por ejemplo, si quieres que la suma se haga antes en (2 + 3) × 4, los paréntesis indican que primero sumes (2 + 3 = 5) y luego multipliques (5 × 4 = 20).
Contenido
¿Por qué es importante el orden de las operaciones?
El orden de las operaciones es fundamental para que las matemáticas sean claras y consistentes. Sin estas reglas, una misma expresión podría tener muchos resultados diferentes, lo que causaría mucha confusión.
Propiedades de las operaciones
Las propiedades conmutativa y asociativa de la suma y la multiplicación nos dicen que podemos cambiar el orden de los números sin alterar el resultado. Por ejemplo, 2 + 3 es lo mismo que 3 + 2. Y 2 × 3 es lo mismo que 3 × 2. Por eso decimos que "el orden de los factores no altera el producto".
Es útil pensar en la división como una multiplicación por una fracción (por ejemplo, 3 ÷ 4 es lo mismo que 3 × ¼). Y la resta como una suma de un número negativo (por ejemplo, 3 – 4 es lo mismo que 3 + (–4)). Esto nos ayuda a entender mejor cómo se combinan las operaciones.
Los símbolos de agrupación, como los paréntesis, nos permiten tratar una parte de la expresión como un solo número. Por ejemplo, en (3 + 5)2, primero sumamos 3 + 5 para obtener 8, y luego elevamos 8 al cuadrado (8 × 8 = 64).
Divisiones y fracciones
Cuando escribimos divisiones, usar la línea horizontal de las fracciones es la forma más clara de evitar confusiones. Por ejemplo, es más fácil entender Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1+2}{3+4} que si usáramos solo el signo de división (/).
Si no usamos la línea de fracción, es muy importante usar paréntesis para que quede claro qué se divide entre qué.
Potencias con números negativos
Cuando ves una expresión como −32, la regla general es que la potencia se aplica solo al número, no al signo negativo. Así que, −32 significa 0 − (32), lo que es 0 − 9 = −9.
Sin embargo, si el signo negativo está dentro de un paréntesis, como (−3)2, entonces el signo también se eleva a la potencia. En este caso, (−3) × (−3) = 9.
Algunas calculadoras o programas pueden interpretar esto de manera diferente, por eso es importante saber cómo funciona tu calculadora o usar paréntesis para asegurarte de que el cálculo se haga como tú quieres.
Acrónimos para recordar el orden
Para recordar el orden de las operaciones, se han creado algunos acrónimos o frases cortas. En español, uno común es PAPOMUDAS, que significa:
- Paréntesis
- Potencias
- Multiplicación
- División
- Adición (suma)
- Sustracción (resta)
En inglés, un acrónimo muy conocido es PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction).
Estos acrónimos son útiles como recordatorio, pero lo más importante es entender las reglas y las propiedades de las operaciones para resolver cualquier problema matemático.
Galería de imágenes
Véase también
 En inglés: Order of operations Facts for Kids
En inglés: Order of operations Facts for Kids