Número ordinal (teoría de conjuntos) para niños
En teoría de conjuntos, una rama de las matemáticas que estudia colecciones de objetos, un número ordinal es una forma especial de clasificar cómo están ordenados los elementos de un conjunto. Imagina que tienes una lista de cosas y quieres saber su posición: primero, segundo, tercero, y así sucesivamente. Los números ordinales hacen esto, ¡incluso para listas infinitas!
Fueron creados por un matemático llamado Georg Cantor en 1897.
Los números ordinales que usamos para contar cosas finitas (como 0, 1, 2, 3...) son los mismos que los números naturales. Esto es porque no importa cómo ordenes un grupo pequeño de cosas, siempre se pueden organizar de la misma manera.
Pero cuando hablamos de conjuntos infinitos, los ordinales son muy útiles. Nos permiten ver diferencias en el orden que los números cardinales (que solo cuentan cuántos elementos hay) no pueden. Por ejemplo, solo hay un tipo de infinito que se puede "contar" (como los números naturales), llamado ℵ0. Pero hay muchísimos números ordinales infinitos que se pueden "contar", y cada uno representa una forma diferente de ordenar los números naturales.
Algunos ejemplos de estos ordinales infinitos son:
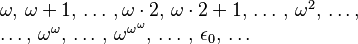
Aquí, la letra griega ω (omega) representa el primer número ordinal infinito.
Contenido
Historia: ¿Quién inventó los números ordinales?
En su trabajo sobre la teoría de conjuntos, Georg Cantor introdujo la idea de los números transfinitos. Estos son como una extensión de los números naturales que conocemos.
Cantor observó que la secuencia de los números naturales:
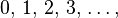
se forma simplemente sumando uno al número anterior. A esto lo llamó el "primer principio de generación".
Pero luego pensó: ¿qué pasa si consideramos un número nuevo, llamado ω, que es más grande que todos los números naturales? Y después de ω, ¿podríamos seguir sumando uno?

Esta nueva secuencia también podría tener un número más grande que todos ellos, que Cantor llamó ω + ω = ω·2.
Así, Cantor introdujo un "segundo principio de generación": si tienes una lista de números que sigue y sigue sin un número final, puedes crear un nuevo número que sea el "límite" de esa lista, es decir, el número inmediatamente mayor que todos ellos.
Esta idea permite continuar la secuencia de números indefinidamente:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0,\,1,\,2,\, \ldots ,\,\omega,\,\omega+1,\, \ldots ,\,\omega\cdot2,\, \ldots ,\,\omega^2,\, \ldots ,\,\omega^\omega,\, \ldots ,
Usando estos números transfinitos, Cantor pudo estudiar el concepto de número ordinal. Un número natural nos dice la posición en una lista (1º, 2º, 3º). Cantor descubrió que cualquier lista ordenada, ya sea finita o infinita, puede ser clasificada por uno de estos números ordinales.
¿Qué es un conjunto bien ordenado?
Para entender los ordinales, primero necesitamos saber qué es un conjunto bien ordenado. Imagina una lista de cosas. Un conjunto está "bien ordenado" si cada vez que tomas un grupo de elementos de esa lista (no importa cuán pequeño o grande sea ese grupo), siempre puedes encontrar un "primer" elemento en ese grupo.
Por ejemplo, los números naturales (0, 1, 2, 3...) están bien ordenados. Si tomas cualquier grupo de números naturales (por ejemplo, {5, 12, 3}), siempre hay un número más pequeño (en este caso, 3).
La importancia de los conjuntos bien ordenados es que nos permiten usar una técnica llamada inducción transfinita, que es como una versión más avanzada de la inducción matemática que se usa para probar cosas sobre los números naturales.
Un número ordinal es un objeto matemático que nos ayuda a clasificar todos los diferentes tipos de conjuntos bien ordenados. Queremos que dos conjuntos que están ordenados de la misma manera (aunque sus elementos sean diferentes) tengan el mismo ordinal.
Ejemplo de ordenación
Las dos formas de ordenar los números naturales que se muestran a continuación son "esencialmente iguales" en cuanto a su orden:
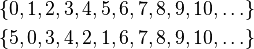
Aunque los números están en un orden diferente al principio, la estructura general de la lista es la misma: siempre hay un primer elemento, un segundo, y así sucesivamente, sin un último elemento.
Sin embargo, si ordenamos los números naturales así:
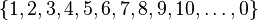
Esto sí es un cambio importante. En esta lista, el número 0 es el último elemento. Las listas anteriores no tenían un último elemento. Esta diferencia en la estructura del orden es lo que los números ordinales nos ayudan a distinguir.
¿Cómo se definen los números ordinales?
Una forma común de definir un ordinal es como un conjunto especial. Un conjunto es un ordinal si cumple dos condiciones importantes:
- Es un conjunto transitivo: esto significa que si un elemento está en el ordinal, y otro elemento está dentro de ese primer elemento, entonces el segundo elemento también debe estar en el ordinal. Es como decir que si A está en B, y B está en C, entonces A también está en C.
- Sus elementos están conectados por la relación de pertenencia: esto significa que si tomas dos elementos diferentes dentro del ordinal, uno siempre será un elemento del otro, o viceversa.
Según esta definición, los números naturales son ordinales. Por ejemplo, el 0 se define como el conjunto vacío ({}). El 1 se define como el conjunto que contiene al 0 ({0}). El 2 se define como el conjunto que contiene al 0 y al 1 ({0, 1}), y así sucesivamente.
De esta definición se puede demostrar que:
- Un ordinal es un conjunto bien ordenado por la relación de "pertenecer a".
- Los elementos de un ordinal son también ordinales. Esto significa que un ordinal es el conjunto de todos los ordinales más pequeños que él.
- La colección de todos los ordinales está bien ordenada.
- Cualquier conjunto bien ordenado es "igual" en su orden a un único ordinal.
- El conjunto de todos los números naturales, , es un ordinal. Es el primer ordinal infinito.
Tipos de ordinales: sucesores y límites
Los ordinales, excepto el cero, se dividen en dos tipos principales:
- Un ordinal sucesor es un ordinal que se obtiene sumando uno a otro ordinal. Por ejemplo, 1 es el sucesor de 0, 2 es el sucesor de 1, y ω+1 es el sucesor de ω. Todos los números naturales mayores que cero son ordinales sucesores.
- Un ordinal límite es un ordinal que no se obtiene sumando uno a ningún otro ordinal. Es como un "límite" de una secuencia de ordinales. El ordinal ω es el primer ordinal límite, porque no hay un ordinal justo antes de él al que se le pueda sumar uno para obtener ω. Es el "límite" de todos los números naturales.
Inducción transfinita
Los números ordinales tienen una propiedad muy útil, similar al principio de inducción que se usa con los números naturales. Si una propiedad es verdadera para el 0, y si es verdadera para un ordinal siempre que sea verdadera para todos los ordinales que vienen antes, entonces esa propiedad es verdadera para todos los ordinales.
Esto nos permite probar cosas sobre todos los ordinales, incluso los infinitos. También nos permite definir funciones sobre los ordinales, paso a paso, usando lo que ya sabemos de los ordinales anteriores.
Operaciones con ordinales
Podemos definir operaciones como la suma, la multiplicación y la potencia para los números ordinales. Estas operaciones extienden las que ya conocemos para los números naturales. Sin embargo, la forma en que funcionan puede ser un poco diferente para los ordinales infinitos. Por ejemplo, para los números naturales, 2 + 3 es lo mismo que 3 + 2. Pero con los ordinales infinitos, 1+ω no es lo mismo que ω+1.
Galería de imágenes
Véase también
 En inglés: Ordinal number Facts for Kids
En inglés: Ordinal number Facts for Kids


