Número de Graham para niños
El número de Graham, nombrado así por el matemático Ronald Graham, es un número increíblemente grande. Se hizo famoso porque, por un tiempo, fue el número más grande usado en una demostración matemática seria.
En 1977, un escritor llamado Martin Gardner lo describió en la revista Scientific American. Dijo que era "una cota tan vasta que tiene el registro de ser el mayor número jamás usado en una demostración matemática seria". El Libro Guinness de los récords también lo mencionó en 1980, lo que ayudó a que la gente se interesara por él.
El número de Graham es mucho, mucho más grande que otros números grandes que quizás conozcas, como el gúgol o el gúgolplex. Es tan gigantesco que no podríamos escribirlo con todos sus dígitos, ni siquiera si usáramos todo el espacio de nuestro universo. Para entenderlo, los matemáticos usan formas especiales de escribir números muy grandes, como la notación flecha de Knuth.
Aunque el número de Graham fue el más grande por un tiempo, hoy en día se han usado números aún mayores en otras demostraciones matemáticas.
Contenido
¿Para qué sirve el número de Graham?
El número de Graham está relacionado con un problema de matemáticas llamado el "problema de Graham", que es parte de una rama de las matemáticas conocida como la teoría de Ramsey. Esta teoría estudia cuándo el orden aparece en sistemas grandes y complejos.
El problema del hipercubo
Imagina un hipercubo (una figura geométrica con muchas dimensiones, como un cubo pero en más de 3D). Este problema pregunta:
- Si conectamos todos los puntos (vértices) de un hipercubo de n dimensiones para formar un grafo completo (donde cada punto está conectado con todos los demás).
- Y luego pintamos cada una de esas conexiones (aristas) de color negro o rojo.
- ¿Cuál es el tamaño más pequeño de n (el número de dimensiones) para que siempre encontremos un grupo de 4 puntos conectados entre sí, donde todas sus conexiones son del mismo color y forman un plano?
Graham y otro matemático, Rothschild, demostraron que este problema tiene una solución. El número de Graham es un límite superior para esa solución, lo que significa que la respuesta es igual o menor que el número de Graham. Más tarde, otro matemático, Exoo, descubrió que la solución es al menos 11. Así que, la respuesta a este problema está entre 11 y el número de Graham.
¿Cómo se define el número de Graham?
El número de Graham, que se representa con la letra G, se define usando la notación flecha de Knuth. Esta notación es una forma de escribir números muy grandes que crecen mucho más rápido que la exponenciación (como 3 elevado a la 3, que es 3x3x3=27).
La notación de flechas funciona así:
- `3 ↑ 3` es 3 elevado a 3 (3^3 = 27)
- `3 ↑↑ 3` es 3 elevado a 3 elevado a 3 (3^(3^3) = 3^27 = 7.625.597.484.987)
- `3 ↑↑↑ 3` es 3 con `3 ↑↑ 3` flechas. Esto significa una "torre" de 3s, donde la altura de la torre es `3 ↑↑ 3`.
El número de Graham se construye en 64 pasos. Imagina una secuencia de números:
- El primer número, llamado g1, es `3 ↑↑↑↑ 3` (tres con cuatro flechas entre los treses).
- El segundo número, g2, es `3` con g1 flechas entre los treses.
- Y así sucesivamente, hasta llegar a G = g64, que es `3` con g63 flechas entre los treses.
Esto significa que el número de flechas en cada paso es el resultado del paso anterior, ¡lo que hace que el número crezca a una velocidad asombrosa!
La magnitud del número de Graham
Es muy difícil entender lo grande que es el número de Graham. Incluso el primer paso de su definición (g1) es un número tan inmenso que no podemos ni imaginarlo.
Para que te hagas una idea, g1 es una "torre de exponentes" de 3s, donde la altura de esa torre es, a su vez, una torre de 3s de una altura gigantesca. ¡El número de 3s en esa torre es mucho mayor que el número de partículas más pequeñas que existen en todo el universo observable!
Y recuerda, g1 es solo el primer paso de 64 pasos para llegar al número de Graham. Esto te da una idea de por qué es tan famoso por su tamaño.
Las últimas cifras del número de Graham
Aunque el número de Graham es incomprensiblemente grande, podemos saber cuáles son sus últimas cifras. Esto se debe a que, cuando tienes una "torre de exponentes" de la forma 3 elevado a 3 elevado a 3... (con muchos 3s), las últimas cifras empiezan a repetirse en un patrón.
Por ejemplo, si miras solo la última cifra de 3, 3^3, 3^(3^3), etc., verás que se repiten en un ciclo. Para el número de Graham, que es una torre muy, muy alta, las últimas cifras se estabilizan.
Aquí tienes una tabla que muestra cómo las últimas cifras se vuelven predecibles a medida que la "torre" de 3s se hace más alta:
| Número de cifras (d) | 3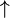 x x |
3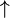 3 3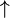 x x |
3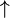 3 3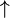 3 3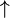 x x |
3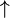 3 3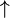 3 3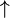 3 3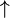 x x |
3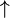 3 3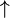 3 3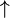 3 3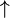 3 3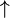 x x |
|---|---|---|---|---|---|
| 1 | 4 (1,3,9,7) |
2 (3,7) |
1 (7) |
1 (7) |
1 (7) |
| 2 | 20 (01,03,...,87,...,67) |
4 (03,27,83,87) |
2 (27,87) |
1 (87) |
1 (87) |
| 3 | 100 (001,003,...,387,...,667) |
20 (003,027,...387,...,587) |
4 (027,987,227,387) |
2 (987,387) |
1 (387) |
Las últimas cifras que son iguales para todas las torres de 3s "suficientemente altas" están en negrita.
Usando un cálculo especial, se ha determinado que las cien últimas cifras del número de Graham son:
...9404248265018193851562535 7963996189939679054966380 0322234872396701848518643 9059104575627262464195387.
Galería de imágenes
Véase también
 En inglés: Graham's number Facts for Kids
En inglés: Graham's number Facts for Kids
Enlaces externos
En inglés:
- "A Ramsey Problem on Hypercubes", por Geoff Exoo
- Weisstein, Eric W. «El número de Graham». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
pl:Notacja strzałkowa#Liczba Grahama

