Negación lógica para niños
Datos para niños Negación |
||
|---|---|---|
 Diagrama de Venn de la conectiva
|
||
| Nomenclatura | ||
| Otros nombres | Negación lógica Complemento lógico |
|
| Lenguaje natural | no A | |
| Lenguaje formal | 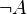 |
|
| Otros símbolos | 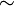 |
|
| Tabla de verdad | ||
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c||c} A & \lnot A \ \hline V & F \ F & V \ \end{array} | ||
En lógica y matemática, la negación es una operación que cambia el significado de una idea o afirmación. Imagina que tienes una frase que es verdadera; al aplicarle la negación, esa frase se vuelve falsa. Y si la frase original era falsa, al negarla se convierte en verdadera. Es como decir "no" a algo.
Por ejemplo, si decimos "El cielo es azul", esta afirmación es verdadera. Si la negamos, diríamos "El cielo no es azul", lo cual es falso. Si la frase fuera "Los perros vuelan" (falsa), al negarla diríamos "Los perros no vuelan" (verdadera).
Contenido
¿Qué es la negación en lógica?
La negación es una de las operaciones más básicas en lógica. Se usa para invertir el valor de verdad de una proposición (una afirmación que puede ser verdadera o falsa). En la lógica clásica, que es la más común, la negación simplemente cambia "verdadero" por "falso" y "falso" por "verdadero".
¿Cómo funciona la negación?
Para entenderlo mejor, podemos usar una tabla de verdad. Una tabla de verdad muestra todos los posibles resultados de una operación lógica.
| p (Proposición) | ¬p (Negación de p) |
|---|---|
| Verdadero | Falso |
| Falso | Verdadero |
En esta tabla, "p" representa cualquier afirmación. "¬p" (que se lee "no p") es la negación de esa afirmación. Como puedes ver, si "p" es verdadera, "¬p" es falsa. Y si "p" es falsa, "¬p" es verdadera.
¿Cómo se escribe la negación?
La negación de una afirmación "p" se puede escribir de varias maneras, dependiendo del contexto o del campo de estudio. Aquí te mostramos algunas de las más comunes:
| Símbolo | Cómo se lee |
|---|---|
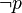 |
no p |
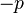 |
no p |
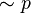 |
no p |
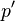 |
p prima |
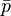 |
p barra |
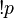 |
exclamación p |
En general, no importa el símbolo que se use, la negación de "p" siempre significa "no es el caso que p" o "no es cierto que p".
Propiedades importantes de la negación
La negación tiene algunas características especiales que la hacen muy útil en lógica y matemáticas.
¿Qué es la doble negación?
La doble negación significa negar una afirmación dos veces. Por ejemplo, si decimos "No es cierto que no llueve", esto es lo mismo que decir "Llueve". En la lógica clásica, negar algo dos veces te devuelve a la afirmación original. Se escribe así: ¬(¬p) es lo mismo que p.
Piensa en ello como si estuvieras dando un giro de 180 grados. Si giras 180 grados una vez, miras en la dirección opuesta. Si giras otros 180 grados, vuelves a mirar en la dirección original.
¿Qué son las leyes de De Morgan?
Las leyes de De Morgan son reglas que nos ayudan a entender cómo la negación se relaciona con otras operaciones lógicas como "y" (conjunción) y "o" (disyunción).
- Si niegas "A o B", es lo mismo que decir "no A y no B".
* Ejemplo: "No es cierto que (está lloviendo o hace frío)" es igual a "No está lloviendo y no hace frío".
- Si niegas "A y B", es lo mismo que decir "no A o no B".
* Ejemplo: "No es cierto que (es de día y hace calor)" es igual a "No es de día o no hace calor".
La negación en la programación
La negación es muy importante en la programación de computadoras. Se usa para crear condiciones lógicas que controlan cómo se comporta un programa.
Por ejemplo, en muchos lenguajes de programación como C++, Java o Python, el símbolo "!" se usa para la negación.
if (!(temperatura > 25))
{
// Este código se ejecuta si la temperatura NO es mayor de 25 grados.
// Es decir, si la temperatura es 25 grados o menos.
}En este ejemplo, `!(temperatura > 25)` significa "no es cierto que la temperatura sea mayor de 25". Esto es muy útil para que los programas tomen decisiones.
También existe la negación a nivel de bits. Esta operación trabaja directamente con los números en su forma binaria (ceros y unos). Cambia cada 1 por un 0 y cada 0 por un 1. Es como voltear cada interruptor individualmente.
Véase también
 En inglés: Negation Facts for Kids
En inglés: Negation Facts for Kids
Galería de imágenes


