Inductancia para niños
En el mundo de la electrónica y el electromagnetismo, la inductancia es una propiedad especial de los componentes llamados inductores o bobinas. Imagina que la inductancia es como la "resistencia al cambio" de la corriente eléctrica. Un inductor es un cable enrollado muchas veces, como un muelle. Cuando la corriente eléctrica intenta cambiar en este cable, el inductor se opone a ese cambio y, al hacerlo, almacena energía en un campo magnético.
La inductancia se representa con la letra L y se mide en una unidad llamada "henrio" (H), en honor al científico estadounidense Joseph Henry. Un henrio es una unidad grande, por lo que a menudo verás valores en milihenrios (mH) o microhenrios (µH).
La cantidad de inductancia de una bobina depende de varias cosas:
- Número de vueltas: Cuantas más vueltas tenga el cable, mayor será la inductancia.
- Forma y tamaño: La forma en que está enrollado el cable y su tamaño también influyen.
- Material del núcleo: Si la bobina tiene un material especial en su centro (como un núcleo de ferrita), la inductancia puede aumentar mucho.
Cuando la corriente eléctrica cambia en una bobina, se produce un voltaje (o tensión eléctrica) en ella. Este voltaje se opone al cambio de corriente. La relación entre el voltaje (V), la inductancia (L) y el cambio de corriente a lo largo del tiempo (ΔI/Δt) se puede expresar con esta fórmula:
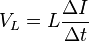
Esto significa que si la corriente cambia rápidamente (ΔI/Δt es grande), el voltaje inducido también será grande.
El término "inductancia" fue usado por primera vez por Oliver Heaviside en 1886. El símbolo L se usa en honor al físico Heinrich Lenz. La inductancia siempre es un valor positivo. Los valores prácticos pueden ir desde muy pequeños (para un cable corto) hasta muy grandes (para bobinas con miles de vueltas y núcleos especiales).
Contenido
Historia de la Inductancia
La historia de la inducción electromagnética, que es una parte del electromagnetismo, comenzó hace mucho tiempo con observaciones simples. Por ejemplo, la carga eléctrica (como la electricidad estática al frotar seda con ámbar), la corriente eléctrica (como un relámpago) y la atracción magnética (como la de una piedra imán). La idea de que todas estas fuerzas de la naturaleza estaban conectadas y la teoría científica del electromagnetismo empezaron a desarrollarse a finales del siglo XVIII.
Descubrimiento de Michael Faraday
La inducción electromagnética fue descubierta por primera vez por Michael Faraday en 1831. En uno de sus experimentos, Faraday enrolló dos cables en lados opuestos de un anillo de hierro. Él pensaba que si la corriente empezaba a fluir en un cable, una especie de "onda" viajaría a través del anillo y causaría un efecto eléctrico en el otro lado.
Usando un galvanómetro (un aparato para detectar corriente), Faraday notó que una corriente eléctrica aparecía por un momento en la segunda bobina cada vez que conectaba o desconectaba una batería de la primera bobina. Esta corriente se producía por el cambio en el flujo magnético que ocurría al conectar y desconectar la batería. Faraday hizo otros descubrimientos importantes sobre la inducción electromagnética, como generar una corriente constante al girar un disco de cobre cerca de una barra magnética.
Tipos de Inductancia
Existen dos tipos principales de inductancia: la autoinductancia y la inductancia mutua.
Autoinductancia: ¿Cómo se afecta una bobina a sí misma?
La autoinductancia es la propiedad de una bobina de generar un voltaje en sí misma cuando la corriente que la atraviesa cambia. Es como si la bobina "se resistiera" a los cambios en su propia corriente. El valor de la autoinductancia de una bobina depende de su forma, tamaño, el número de vueltas y el material de su núcleo.
Por ejemplo, para un solenoide (una bobina larga y recta), la autoinductancia (L) se puede calcular con una fórmula que incluye la permeabilidad magnética del material del núcleo (μ), el número de vueltas (N), el área de la sección transversal de la bobina (A) y su longitud (l):
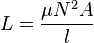
Esta fórmula nos muestra que la autoinductancia aumenta si la bobina tiene más vueltas, un área más grande o un material de núcleo que permite que el campo magnético se forme más fácilmente.
Inductancia Mutua: ¿Cómo se afectan las bobinas entre sí?
La inductancia mutua ocurre cuando el campo magnético creado por una bobina afecta a otra bobina cercana. Si la corriente cambia en la primera bobina, su campo magnético cambiante puede inducir un voltaje en la segunda bobina. Es como si las bobinas estuvieran "conectadas" magnéticamente.
Este efecto puede ser intencional, como en los transformadores, que usan la inductancia mutua para cambiar los niveles de voltaje. Pero a veces, este acoplamiento magnético no es deseado y puede causar problemas en los circuitos.
La inductancia mutua se representa con la letra M. En un sistema de dos bobinas, tendríamos:
- L₁₁: La autoinductancia de la bobina 1.
- L₂₂: La autoinductancia de la bobina 2.
- M: La inductancia mutua entre la bobina 1 y la bobina 2.
El coeficiente de acoplamiento magnético (K) nos dice qué tan fuerte es la conexión magnética entre dos bobinas. Su valor va de 0 (sin acoplamiento) a 1 (acoplamiento perfecto). Se calcula con la fórmula:
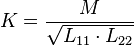
Autoinducción en Formas de Alambre Delgado
La siguiente tabla muestra fórmulas para calcular la autoinductancia de algunas formas simples hechas con cables delgados. Estas fórmulas son más precisas cuando el radio del cable es mucho más pequeño que las dimensiones de la forma y cuando no hay materiales magnéticos cerca.
| Tipo | Inductancia | Comentario |
|---|---|---|
| Solenoide de una sola capa |
La fórmula de Wheeler para bobinas de aire: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L} = \frac{N^2 D^2}{18D + 40\ell} (pulgadas) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L} = \frac{N^2 D^2}{45D + 100\ell} (cm) Esta fórmula tiene un error de menos del 1% cuando la longitud es mayor a 0.4 veces el diámetro. |
|
| Cable coaxial (alta frecuencia) |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L} = \frac{\mu_0}{2\pi} \ell \ln\left(\frac{b}{a}\right) |
|
| Bucle circular | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L} = \mu_0\ r\ \left[\ln\left(\frac{8 r}{a}\right) - 2 + \tfrac{1}{4}Y + \mathcal{O} \left(\frac{a^2}{r^2}\right)\right] |
|
| Rectángulo de alambre redondo |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \mathcal{L} = \frac{\mu_0}{\pi}\ \biggl[\ &\ell_1\ln\left(\frac{2\ell_1}{a}\right) + \ell_2\ \ln\left(\frac{2\ell_2}{a}\right) + 2\sqrt{\ell_1^2 + \ell_2^2\ } \\ &- \ell_1\ \sinh^{-1}\left(\frac{\ell_1}{\ell_2}\right) - \ell_2 \sinh^{-1}\left(\frac{\ell_2}{\ell_1}\right) \\ &- \left(2 - \tfrac{1}{4}Y\ \right)\left(\ell_1 + \ell_2\right)\ \biggr] \end{align} |
|
| Par de cables paralelos |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{L} = \frac{\ \mu_0 }{\pi}\ \ell\ \left[ \ln\left(\frac{s}{a}\right) + \tfrac{1}{4}Y \right] |
|
| Par de cables paralelos (alta frecuencia) |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \mathcal{L} &= \frac{\mu_0}{\pi}\ \ell\ \cosh^{-1}\left(\frac{s}{2a}\right) \\ &= \frac{\mu_0}{\pi}\ \ell\ \ln\left(\frac{s}{2a} + \sqrt{\frac{s^2}{4a^2} - 1}\right) \\ &\approx \frac{\mu_0}{\pi}\ \ell\ \ln\left(\frac{s}{a}\right) \end{align} |
|
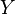 es un valor entre 0 y 1 que depende de cómo se distribuye la corriente en el cable. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Y = 0 cuando la corriente fluye solo por la superficie del cable (esto se llama efecto de piel), y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Y = 1 cuando la corriente se distribuye de manera uniforme por todo el cable (como en la corriente continua).
es un valor entre 0 y 1 que depende de cómo se distribuye la corriente en el cable. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Y = 0 cuando la corriente fluye solo por la superficie del cable (esto se llama efecto de piel), y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Y = 1 cuando la corriente se distribuye de manera uniforme por todo el cable (como en la corriente continua).
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathcal{O}(x) representa términos pequeños que se han quitado de la fórmula para hacerla más sencilla. Significa "más pequeñas correcciones que varían en el orden de  ".
".
Véase también
 En inglés: Inductor Facts for Kids
En inglés: Inductor Facts for Kids



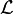 inductancia en μH (microhenrios)
inductancia en μH (microhenrios)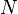 número de vueltas
número de vueltas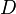 diámetro en pulgadas o cm
diámetro en pulgadas o cm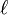 longitud en pulgadas o cm
longitud en pulgadas o cm : Radio interior del conductor exterior
: Radio interior del conductor exterior : Radio del conductor interior
: Radio del conductor interior : Radio del bucle
: Radio del bucle : Distancia de separación, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): s \ge 2a
: Distancia de separación, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): s \ge 2a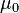 : ver notas al pie de la tabla.
: ver notas al pie de la tabla.