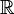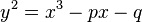Curva elíptica para niños
En matemáticas, las curvas elípticas son formas especiales que se dibujan usando ecuaciones cúbicas (de tercer grado). Aunque se llaman "elípticas", ¡no son elipses! Son diferentes.
Estas curvas son muy útiles. Por ejemplo, ayudaron a demostrar el famoso último teorema de Fermat. También se usan para encontrar los factores de números muy grandes, un proceso llamado factorización de enteros. Además, son clave en la criptografía de curvas elípticas, que es una forma de proteger información secreta.
Las curvas elípticas son "suaves", lo que significa que no tienen esquinas puntiagudas ni se cruzan a sí mismas. En ellas, se puede definir una forma especial de "sumar" puntos, lo que las convierte en un grupo abeliano en matemáticas.
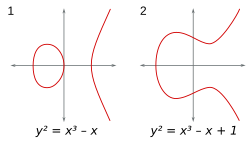
Algunos ejemplos de estas curvas sobre los números reales (los números que usamos normalmente) son las que tienen ecuaciones como 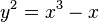 y
y 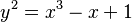 .
.
Contenido
¿Qué son las curvas elípticas?
Definición matemática sencilla
Las curvas elípticas se pueden definir sobre diferentes tipos de sistemas numéricos, no solo los números reales. Formalmente, una curva elíptica es una curva algebraica especial que no tiene puntos "problemáticos" (como esquinas o cruces) y que cumple ciertas propiedades matemáticas.
Si el sistema numérico no es muy complicado (es decir, su "característica" no es 2 ni 3), cualquier curva elíptica se puede escribir con una ecuación parecida a esta:
Aquí, 'p' y 'q' son números de ese sistema. Lo importante es que la parte derecha de la ecuación (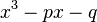 ) no tenga raíces repetidas. La curva está formada por todos los puntos (x,y) que cumplen esta ecuación.
) no tenga raíces repetidas. La curva está formada por todos los puntos (x,y) que cumplen esta ecuación.
¿Cómo se "suman" puntos en una curva elíptica?
La ley de grupo: una forma especial de sumar
Imagina que a la curva le añadimos un punto especial que llamamos el "punto en el infinito". Con este punto, podemos definir una operación de "suma" entre los puntos de la curva.
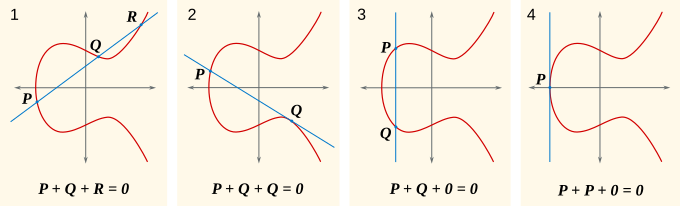
La idea es así: si tienes dos puntos, P y Q, en la curva, puedes dibujar una línea recta que los una. Esa línea cruzará la curva en un tercer punto, llamémoslo R. Si la línea es tangente a la curva en un punto, ese punto cuenta dos veces. Si la línea es vertical, el tercer punto es el "punto en el infinito".
En este sistema, el "punto en el infinito" actúa como el "cero" o la identidad del grupo. La regla para sumar es que si una línea recta pasa por los puntos P, Q y R de la curva, entonces P + Q + R = 0 (donde 0 es el punto en el infinito).
Esta forma de "sumar" hace que el conjunto de puntos de la curva (incluyendo el punto en el infinito) se comporte como un grupo abeliano. Esto significa que la suma es asociativa (no importa cómo agrupes los puntos al sumar), tiene un elemento neutro (el punto en el infinito) y cada punto tiene un "opuesto" (su inverso).
Suma de puntos con fórmulas
Para entenderlo mejor, veamos cómo se suman los puntos P = (xP, yP) y Q = (xQ, yQ) en una curva como y2 = x3 - px - q.
- Si las coordenadas 'x' de los puntos son diferentes (xP ≠ xQ):
* Calculamos una pendiente 's' como: s = (yP - yQ) / (xP - xQ). * El punto resultante R = P + Q = (xR, yR) se calcula con estas fórmulas: * 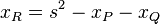 *
* 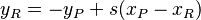
- Si las coordenadas 'x' son iguales (xP = xQ):
* Si las coordenadas 'y' son opuestas (yP = -yQ): La suma de los puntos es el "punto en el infinito" (0). Esto significa que el opuesto de un punto se encuentra reflejándolo sobre el eje 'x'. * Si las coordenadas 'y' son iguales y no son cero (yP = yQ ≠ 0): Esto es como sumar un punto consigo mismo (2P). * Calculamos una pendiente 's' (que es la pendiente de la tangente a la curva en ese punto): s = (3xP2 - p) / (2yP). * El punto resultante R = 2P = (xR, yR) se calcula con estas fórmulas: * 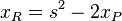 *
* 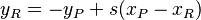 * Si las coordenadas 'y' son iguales y son cero (yP = yQ = 0): La suma de los puntos es el "punto en el infinito" (0).
* Si las coordenadas 'y' son iguales y son cero (yP = yQ = 0): La suma de los puntos es el "punto en el infinito" (0).
Usos importantes de las curvas elípticas
Aplicaciones prácticas
Las curvas elípticas sobre sistemas numéricos finitos (que tienen un número limitado de elementos) son muy importantes en la actualidad. Se utilizan en varias áreas, como:
- Criptografía: Son la base de la criptografía de curvas elípticas, un método muy seguro para proteger la información digital. Muchos sistemas de seguridad en internet, como los que protegen tus mensajes o tus compras en línea, usan esta tecnología. La idea es que, si un algoritmo usa ciertos grupos matemáticos, podemos adaptarlo para que use los grupos de puntos de curvas elípticas, lo que a menudo lo hace más eficiente y seguro.
- Factorización de enteros: También se emplean en algoritmos para encontrar los factores primos de números muy grandes, como el Factorización de curva elíptica de Lenstra.
Conexiones con otros teoremas
Las curvas elípticas también están relacionadas con teoremas matemáticos muy complejos:
- El teorema de Mordell-Weil dice que si trabajamos con números racionales (fracciones), el grupo de puntos de la curva que son racionales tiene una estructura especial.
- La demostración del último teorema de Fermat (que dice que no hay números enteros positivos a, b, c que cumplan an + bn = cn para n mayor que 2) se logró gracias a una conexión profunda entre las curvas elípticas y las "formas modulares".
Véase también
 En inglés: Elliptic curve Facts for Kids
En inglés: Elliptic curve Facts for Kids