Distribución binomial para niños
Datos para niños Distribución binomial |
||
|---|---|---|
|
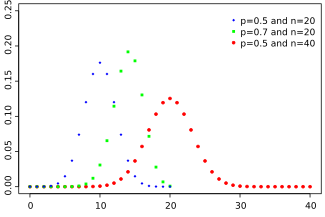
Función de masa de probabilidad Función de probabilidad |
||
|
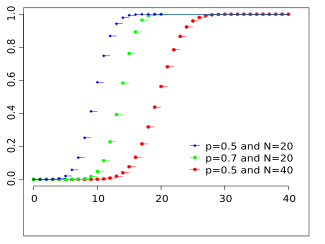
Función de distribución acumulada Función de distribución de probabilidad |
||
| Parámetros | 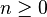 número de ensayos (entero) número de ensayos (entero)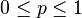 probabilidad de éxito (real) probabilidad de éxito (real) |
|
| Dominio | 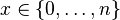 |
|
| Función de probabilidad (fp) | 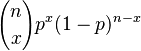 |
|
| Función de distribución (cdf) | 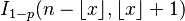 |
|
| Media | 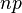 |
|
| Mediana | Uno de 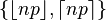 |
|
| Moda | 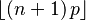 |
|
| Varianza | 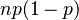 |
|
| Coeficiente de simetría |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1-2p}{\sqrt{np(1-p)</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END-->\! |curtosis = La distribución binomial es una herramienta de la teoría de la probabilidad y la estadística. Nos ayuda a calcular la probabilidad de obtener un cierto número de "éxitos" en una serie de intentos. Imagina que repites un experimento varias veces, y en cada intento solo hay dos resultados posibles: "éxito" o "fracaso". La probabilidad de "éxito" debe ser siempre la misma en cada intento. Por ejemplo, si lanzas una moneda varias veces, cada lanzamiento es un intento. Obtener "cara" podría ser un "éxito" y "cruz" un "fracaso". La distribución binomial nos diría cuál es la probabilidad de obtener un número específico de "caras" en esos lanzamientos. Esta distribución se usa mucho para entender situaciones donde hay dos resultados posibles. Es una de las primeras leyes de probabilidad que se estudian. ContenidoDistribución Binomial: Contando ÉxitosLa distribución binomial nos permite saber cuántas veces esperamos que ocurra un "éxito" en un número fijo de intentos. Cada intento es independiente de los demás. Esto significa que el resultado de un intento no afecta el resultado del siguiente. ¿Qué es un Experimento Binomial?Un experimento binomial tiene algunas características importantes:
Cuando se cumplen estas condiciones, decimos que la variable que cuenta el número de éxitos sigue una distribución binomial. Ejemplos SencillosAquí tienes algunos ejemplos para entenderlo mejor: Lanzar una MonedaImagina que lanzas una moneda 10 veces. Quieres saber cuántas veces saldrá "cara".
La distribución binomial te ayudaría a calcular la probabilidad de obtener, por ejemplo, 7 caras en esos 10 lanzamientos. Lanzar un DadoAhora, piensa que lanzas un dado de 6 caras 5 veces. Quieres saber cuántas veces saldrá el número 3.
La distribución binomial te diría la probabilidad de que el 3 aparezca, por ejemplo, 2 veces en los 5 lanzamientos. ¿Cómo se Calcula la Probabilidad?Para calcular la probabilidad de obtener exactamente k éxitos en n intentos, usamos una fórmula especial: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{P}(X = k)= {n \choose k} \, p^k (1-p)^{n-k}. En esta fórmula:
Por ejemplo, si lanzas un dado 51 veces y quieres saber la probabilidad de que el número 3 salga 20 veces:
Usando la fórmula, la probabilidad sería: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{P}[X=20]={51 \choose 20}(1/6)^{20}(5/6)^{51-20}=0.0000744 \,\! Esto significa que es muy poco probable que el 3 salga exactamente 20 veces. ¿Para Qué Sirve la Distribución Binomial?La distribución binomial es muy útil en muchos campos. Por ejemplo:
Es una base importante para entender cómo el azar afecta los resultados y para tomar decisiones basadas en datos. Propiedades ImportantesCuando una variable sigue una distribución binomial, podemos calcular algunas cosas interesantes sobre ella. Media y Varianza
Relación con Otras DistribucionesLa distribución binomial está relacionada con otras distribuciones de probabilidad. La Distribución de BernoulliLa distribución de Bernoulli es un caso especial de la distribución binomial. Ocurre cuando solo hay un intento (n = 1). Es decir, si haces un solo experimento con dos resultados posibles, eso es una distribución de Bernoulli. Aproximaciones ÚtilesA veces, cuando el número de intentos (n) es muy grande, calcular las probabilidades con la fórmula binomial puede ser complicado. En esos casos, podemos usar otras distribuciones para aproximar los resultados:
Estas aproximaciones nos ayudan a hacer cálculos más sencillos sin perder mucha precisión. Galería de imágenesVéase también
|
|


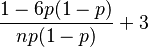 |entropía =
|entropía = 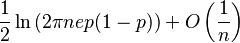 |mgf =
|mgf = 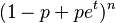 |car =
|car = 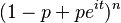 }}
}}
 es la probabilidad de fracaso en un solo intento.
es la probabilidad de fracaso en un solo intento. es el coeficiente binomial. Se calcula como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{n!}{k!(n-k)!} y representa el número de formas diferentes en que puedes obtener k éxitos en n intentos.
es el coeficiente binomial. Se calcula como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{n!}{k!(n-k)!} y representa el número de formas diferentes en que puedes obtener k éxitos en n intentos.![\operatorname{E}[X] = np](/images/math/9/e/d/9ed22d6f166c0c97bf4d3df33869a744.png) Por ejemplo, si lanzas una moneda 100 veces, esperas obtener 100 * 0.5 = 50 caras.
Por ejemplo, si lanzas una moneda 100 veces, esperas obtener 100 * 0.5 = 50 caras.![\operatorname{Var}[X] =np(1-p)](/images/math/2/e/4/2e4032668ef633c5a68e9669ff8536f2.png)
 En inglés:
En inglés: