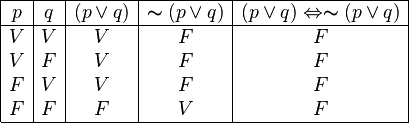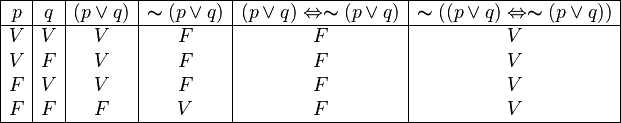Contradicción para niños
Datos para niños Contradicción |
||
|---|---|---|
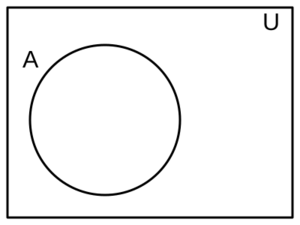
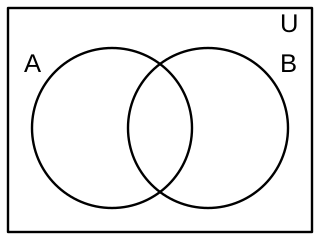 Diagrama de Venn de la conectiva
|
||
| Nomenclatura | ||
| Lenguaje formal |  |
|
| Tabla de verdad | ||
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c|c||c} A & B & \bot \ \hline V & V & F \ V & F & F \ F & V & F \ F & F & F \ \end{array} | ||
En lógica, una contradicción ocurre cuando dos o más ideas o afirmaciones no pueden ser ciertas al mismo tiempo. Es como decir algo que se anula a sí mismo. Por ejemplo, las frases "llueve y no llueve" o "ni llueve ni truena, pero llueve y truena" son contradicciones. Son imposibles en la realidad.
Contenido
¿Qué es una Contradicción?
Una contradicción es una situación donde una afirmación es verdadera y falsa a la vez. Esto no puede pasar en la lógica. Es un concepto fundamental para entender cómo funciona el razonamiento.
Contradicciones en la Lógica
En la lógica proposicional, una contradicción es una frase o fórmula que siempre resulta falsa. Esto ocurre sin importar si las partes de la frase son verdaderas o falsas. Siempre nos dará un resultado "falso".
¿Cómo funcionan las Tablas de Verdad?
Las tablas de verdad son herramientas que nos ayudan a ver si una afirmación es verdadera o falsa. Muestran todos los posibles resultados de una frase lógica. Para una contradicción, la tabla siempre mostrará "Falso" (F) en el resultado final.
Contradicciones con una variable
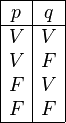
Imagina que tenemos una afirmación simple, como "p". Esta afirmación puede ser verdadera (V) o falsa (F).
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{|c|} \hline p \\ \hline V \\ F \\ \hline \end{array}
Ahora, si combinamos "p" con "no p" (que se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \thicksim p ), obtenemos una contradicción. Por ejemplo, "llueve y no llueve".
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{|c|c|c|} \hline p & \thicksim p & p \land \thicksim p \\ \hline V & F & F \\ F & V & F \\ \hline \end{array}
Como puedes ver, el resultado final (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p \land \thicksim p ) siempre es Falso.
Contradicciones con dos variables
También podemos tener contradicciones con más de una afirmación. Por ejemplo, con dos afirmaciones, "p" y "q".
La siguiente tabla muestra una contradicción más compleja. Aquí, la afirmación final siempre es Falsa.
Contradicción y Tautología: ¿Son opuestas?
Sí, una contradicción es lo opuesto a una tautología. Una tautología es una afirmación que siempre es verdadera. Si niegas una contradicción, obtendrás una tautología. Y si niegas una tautología, obtendrás una contradicción.
Por ejemplo, si negamos la contradicción anterior, obtenemos una tautología:
Como puedes ver, el resultado final ahora siempre es Verdadero (V).
La Contradicción en la Lógica de Proposiciones
En la lógica, podemos representar la contradicción con un símbolo especial:  . Este símbolo significa que una afirmación es siempre falsa, sin importar qué. Los diagramas de Venn también pueden mostrar esto. En ellos, una contradicción se ve como un espacio vacío, indicando que no hay ninguna situación en la que sea verdadera.
. Este símbolo significa que una afirmación es siempre falsa, sin importar qué. Los diagramas de Venn también pueden mostrar esto. En ellos, una contradicción se ve como un espacio vacío, indicando que no hay ninguna situación en la que sea verdadera.
Véase también
 En inglés: Contradiction Facts for Kids
En inglés: Contradiction Facts for Kids
- Principio de no contradicción
- Reducción al absurdo
- Cuadro de oposición de los juicios
- Contradictio in adiecto