NP-completo para niños
En el mundo de la complejidad computacional, que estudia lo difíciles que son los problemas para las computadoras, existe un grupo especial de desafíos llamados NP-completo. Imagina que tienes muchos rompecabezas. Los problemas NP-completo son como los rompecabezas más difíciles de un gran grupo llamado NP. Si pudieras encontrar una forma muy rápida de resolver uno de estos rompecabezas NP-completo, ¡entonces podrías resolver rápidamente todos los demás rompecabezas del grupo NP!
Se cree que estos problemas NP-completo son tan difíciles que no existe una forma súper rápida de resolverlos para computadoras normales. Si alguien encontrara una solución rápida para uno de ellos, sería un descubrimiento enorme en la informática.
Un ejemplo de problema NP-completo es el "problema de la suma de subconjuntos". Imagina que tienes una lista de números. La pregunta es: ¿puedes encontrar un grupo de esos números que, al sumarlos, den cero? Es fácil verificar si una respuesta es correcta, pero encontrar ese grupo de números puede ser muy complicado, ¡a veces hay que probar casi todas las combinaciones posibles!
Contenido
¿Qué son los problemas NP-completo?
Los problemas NP-completo son un tipo especial de problema de decisión. Un problema de decisión es aquel que tiene una respuesta de "sí" o "no". Para que un problema sea considerado NP-completo, debe cumplir dos condiciones importantes:
Condiciones para ser NP-completo
- Está en NP: Esto significa que si alguien te da una posible solución al problema, puedes verificar si esa solución es correcta de forma rápida. "Rápida" en este caso significa en "tiempo polinómico", que es una forma técnica de decir que el tiempo que tarda la computadora en verificar la solución no crece demasiado a medida que el problema se hace más grande.
- Es el más difícil de NP: Esto significa que cualquier otro problema en el grupo NP puede ser transformado en este problema NP-completo de forma rápida. Es como si este problema fuera un "problema maestro" al que todos los demás problemas NP pueden ser convertidos.
Si un problema cumple estas dos condiciones, se le llama NP-completo. Esto implica que si encontráramos una manera rápida de resolver un problema NP-completo, automáticamente tendríamos una manera rápida de resolver todos los problemas en el grupo NP.
Esta idea fue propuesta por un científico llamado Stephen Cook en 1971. Al principio, la gente se sorprendió de que existieran problemas así de "maestros". Cook demostró que un problema llamado "problema de satisfacibilidad booleana" es NP-completo. Desde entonces, se han descubierto miles de otros problemas que también pertenecen a esta categoría.
La historia de los problemas NP-completo
El concepto de NP-completo nació gracias a Stephen Cook en 1971. Él presentó sus ideas en una conferencia, y aunque no usó el término "NP-completo" directamente, sentó las bases.
El gran desafío: ¿P es igual a NP?
Después de que Cook presentara su trabajo, hubo un gran debate entre los científicos de la computación. La pregunta clave era: ¿pueden los problemas NP-completo resolverse de forma rápida (es decir, en "tiempo polinómico")? Esta pregunta se conoce como el problema ¿P=NP?.
Hasta el día de hoy, nadie ha podido responder a esta pregunta. Es uno de los problemas no resueltos de la matemática más importantes. Desde el año 2000, una organización llamada Clay Mathematics Institute ofrece un premio de un millón de dólares a quien logre demostrar si P es igual a NP o si P no es igual a NP. ¡Imagínate la importancia de este desafío!
En 1972, otro científico, Richard Karp, demostró que muchos otros problemas comunes también eran NP-completo, basándose en el trabajo de Cook. Esto ayudó a la comunidad científica a entender mejor la dificultad de estos problemas.
Ejemplos de problemas NP-completo
Hay muchos problemas en diferentes áreas que son NP-completo. Aquí te mostramos algunos de los más conocidos:
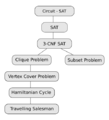
- Problema de satisfacibilidad booleana (SAT): Se trata de encontrar si una fórmula lógica compleja puede ser verdadera.
- Problema de la mochila: Imagina que tienes una mochila con un límite de peso y muchos objetos con diferentes pesos y valores. ¿Qué objetos debes meter en la mochila para llevar el mayor valor posible sin exceder el peso?
- Problema del ciclo hamiltoniano: En un mapa con ciudades y carreteras, ¿puedes encontrar un camino que visite cada ciudad exactamente una vez y regrese al punto de partida?
- Problema del vendedor viajero: Similar al anterior, pero buscando el camino más corto que visite todas las ciudades y regrese al inicio.
- Problema de la clique: En un grupo de personas, ¿cuál es el grupo más grande donde todos se conocen entre sí?
A veces, una pequeña diferencia en un problema puede cambiar si es NP-completo o no. Por ejemplo, colorear un mapa con solo dos colores es fácil para una computadora, pero si te piden usar tres colores, ¡se vuelve un problema NP-completo!
¿Cómo se resuelven los problemas NP-completo?
Dado que no se conoce una forma rápida de resolver los problemas NP-completo para cualquier tamaño, los científicos usan diferentes estrategias:
- Algoritmos de aproximación: Estos algoritmos encuentran una solución que no es perfecta, pero es lo suficientemente buena y se encuentra rápidamente. No todos los problemas NP-completo tienen este tipo de soluciones.
- Algoritmos probabilísticos: Usan la suerte o la aleatoriedad para encontrar una buena solución en promedio, aunque a veces pueden fallar.
- Restricciones: A veces, si el problema tiene una estructura más simple, se pueden encontrar algoritmos más rápidos.
- Casos particulares: Para ciertas versiones muy específicas del problema, puede haber soluciones rápidas.
- Heurísticas: Son métodos que funcionan bien en la práctica para muchos casos, aunque no garantizan la mejor solución. Son como "reglas generales" que suelen dar buenos resultados.
Galería de imágenes
-
Algunos problemas NP-completo y cómo se relacionan entre sí. Las flechas muestran cómo un problema puede transformarse en otro.
Véase también
En inglés: NP-completeness Facts for Kids
