Problema de satisfacibilidad booleana para niños
El Problema de Satisfacibilidad Booleana (conocido como SAT) es un desafío fundamental en el mundo de la computación. Imagina que tienes una frase lógica con variables que pueden ser verdaderas o falsas. El problema SAT consiste en averiguar si existe alguna manera de asignar valores de "verdadero" o "falso" a esas variables para que toda la frase se convierta en "verdadera". Fue el primer problema que se identificó como "NP-completo", un concepto importante en la teoría de la complejidad computacional.
Plantilla:Ficha de problema de decisión
Contenido
¿Qué es el Problema SAT?
El problema SAT se trata de encontrar una solución para una expresión lógica. Piensa en una expresión como una ecuación, pero en lugar de números, usas ideas de "verdadero" y "falso". Las variables en estas expresiones se llaman "booleanas" porque solo pueden tener dos estados: verdadero (1) o falso (0).
Por ejemplo, si tienes la expresión:
El problema SAT te pregunta: ¿Podemos encontrar valores para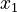 
, 
, 
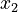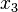y 
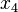(verdadero o falso) para que toda la expresión sea verdadera? Si la expresión nunca puede ser verdadera, no importa qué valores les des a las variables, entonces se le llama UNSAT.
Historia y Descubrimientos Clave
¿Quién descubrió el Problema SAT?
El concepto de "NP-completo" y la importancia del problema SAT fueron establecidos por Stephen Cook en 1971. Su trabajo, conocido como el Teorema de Cook, fue revolucionario porque demostró que SAT era el primer problema de este tipo. Esto significa que si pudieras resolver SAT de forma rápida, podrías resolver muchos otros problemas complejos de la misma manera.
Algoritmos para Resolver SAT
En 1960, los científicos Martin Davis y Hilary Putnam crearon un método para verificar si estas expresiones lógicas podían ser verdaderas. Este método se mejoró en 1962 con el algoritmo DPLL (Davis-Putnam-Logemann-Loveland), que es una forma sistemática de buscar soluciones. Este algoritmo es la base de muchos de los programas modernos que resuelven problemas SAT.
La Complejidad de SAT
¿Por qué es SAT un Problema Difícil?
El problema SAT es considerado "NP-completo" porque, aunque es fácil verificar una solución si ya la tienes, encontrar esa solución puede ser muy difícil y tomar mucho tiempo, especialmente si la expresión tiene muchas variables. Imagina que tienes que probar todas las combinaciones posibles de verdadero y falso para cada variable; el número de combinaciones crece muy rápido.
Variantes del Problema SAT
- 3-SAT: Es una versión especial de SAT donde cada parte de la expresión (llamada "cláusula") tiene exactamente tres variables. Aunque parece más simple, 3-SAT sigue siendo un problema NP-completo. Esto es útil porque si puedes resolver 3-SAT, puedes resolver muchos otros problemas difíciles.
- 2-SAT: En esta versión, cada cláusula tiene un máximo de dos variables. ¡La buena noticia es que 2-SAT es mucho más fácil de resolver! Los programas pueden encontrar una solución en un tiempo razonable, incluso para expresiones grandes.
Algoritmos Modernos para SAT
Hoy en día, existen programas muy avanzados, llamados "solucionadores SAT", que pueden resolver problemas SAT muy grandes y complejos. Estos programas usan versiones mejoradas del algoritmo DPLL, incorporando técnicas inteligentes como:
- Análisis de conflictos: Aprenden de los errores para no repetirlos.
- Aprendizaje de cláusulas: Guardan información sobre partes de la expresión que ya han resuelto.
- Saltos no cronológicos (backjumping): Si llegan a un callejón sin salida, pueden retroceder varios pasos en lugar de solo uno.
- Reinicios aleatorios: A veces, empezar de nuevo desde un punto diferente puede ayudar a encontrar la solución más rápido.
Estos avances han hecho que los solucionadores SAT sean herramientas muy poderosas. Se usan en áreas como el diseño de circuitos electrónicos, la verificación de programas de computadora y la inteligencia artificial. Algunos de estos programas son tan eficientes que pueden resolver problemas enormes en poco tiempo. Un ejemplo es MINISAT, que es muy compacto y ganó una competencia importante en 2005.
|
Véase también
En inglés: 