Problema del viajante para niños
El problema del vendedor viajero (también conocido como el problema del viajante) es un desafío muy interesante en el mundo de las matemáticas y la informática. Imagina que tienes una lista de ciudades y sabes la distancia entre cada par de ellas. La pregunta es: ¿cuál es la ruta más corta posible que visita cada ciudad exactamente una vez y, al final, regresa a la ciudad de donde partió?
Este problema fue planteado por primera vez en 1930 y es uno de los más estudiados en el campo de la optimización. Se usa mucho para probar qué tan buenos son los diferentes métodos que buscan la mejor solución a un problema. Aunque es muy difícil de resolver para las computadoras, existen muchas técnicas que permiten encontrar soluciones para problemas con cientos o incluso miles de ciudades.
Plantilla:Ficha de problema de optimización
Contenido
¿Qué es el Problema del Vendedor Viajero?
El problema del vendedor viajero, a menudo llamado TSP por sus siglas en inglés (Travelling Salesman Problem), busca la ruta más eficiente. Piensa en un repartidor que tiene que entregar paquetes en varias direcciones y quiere gastar la menor gasolina posible. O un robot que debe soldar puntos en una placa electrónica y necesita hacerlo en el menor tiempo.
¿Por qué es tan difícil de resolver?
La dificultad de este problema radica en la enorme cantidad de rutas posibles.
- Si tienes solo 5 ciudades, hay 12 rutas diferentes. ¡No es tan difícil de calcular!
- Pero si tienes 10 ciudades, ¡hay 181.440 rutas diferentes!
- Y si llegas a 30 ciudades, ¡el número de rutas posibles es más de 4.000.000.000.000.000.000.000.000.000.000!
Para que te hagas una idea, si una computadora pudiera calcular un millón de rutas por segundo, ¡necesitaría más de 100.000.000.000.000.000 años para encontrar la mejor ruta para 30 ciudades! Esto es mucho más tiempo del que existe el universo. Por eso, se dice que es un problema "NP-duro", lo que significa que es extremadamente difícil para las computadoras encontrar la solución perfecta cuando el número de ciudades es grande.
¿Para qué se usa este problema?
Aunque parezca un juego de lógica, el problema del vendedor viajero tiene muchas aplicaciones prácticas en el mundo real:
Ejemplos de la vida real
- Planificación de rutas: Empresas de reparto, servicios de transporte público o camiones de basura lo usan para encontrar las rutas más cortas y ahorrar tiempo y combustible.
- Logística: Ayuda a organizar el movimiento de productos en almacenes o entre diferentes puntos de venta.
- Fabricación de circuitos electrónicos: Se utiliza para programar las máquinas que perforan agujeros en las placas de circuitos, asegurando que lo hagan de la manera más rápida.
- Secuenciación de ADN: En la biología, se usa para ordenar fragmentos de ADN, donde las "ciudades" son los fragmentos y las "distancias" son qué tan parecidos son.
- Robótica: Para que los robots realicen tareas en un orden eficiente, como soldar o pintar.
En estas aplicaciones, las "ciudades" pueden ser clientes, puntos de soldadura o fragmentos de ADN, y las "distancias" pueden ser el tiempo de viaje, el costo o la similitud entre elementos.
Historia del Problema del Vendedor Viajero
El origen exacto de este problema no está del todo claro. Ya en 1832, una guía para viajeros mencionaba algo similar al problema, con ejemplos de rutas por Alemania y Suiza, pero sin un enfoque matemático.
El problema fue definido formalmente en el siglo XIX por matemáticos como el irlandés William Rowan Hamilton y el británico Thomas Kirkman. Hamilton incluso creó un juego llamado "Juego Icosian" que se basaba en encontrar un camino específico.
La forma moderna del problema del vendedor viajero comenzó a estudiarse en los años 1930 por matemáticos en Viena y Harvard. Uno de ellos, Karl Menger, notó que la forma más sencilla de resolverlo (probar todas las rutas) era demasiado lenta y que un método simple como ir siempre a la ciudad más cercana no siempre daba la ruta más corta.
Hassler Whitney, de la Universidad de Princeton, le dio el nombre de "problema del vendedor viajero" poco después.
Entre 1950 y 1960, el problema se hizo muy popular entre los científicos. Un gran avance fue el de George Dantzig, Delbert Ray Fulkerson y Selmer M. Johnson de la Corporación RAND. Ellos lograron resolver un problema con 49 ciudades, lo cual fue un gran logro para la época.
En 1972, Richard Karp demostró que el problema del vendedor viajero es "NP-duro", lo que confirmó su gran dificultad computacional.
A finales de los años 70 y principios de los 80, investigadores como Grötschel, Padberg y Rinaldi lograron resolver problemas con hasta 2392 ciudades.
En los años 90, un grupo de científicos desarrolló un programa llamado Concorde, que ha sido clave para resolver los problemas más grandes. En 2006, lograron encontrar la ruta óptima para un problema con 85.900 ciudades, relacionado con el diseño de microchips.
Cómo se intenta resolver
Para abordar un problema tan difícil como el del vendedor viajero, los expertos usan varias estrategias:
- Algoritmos exactos: Son métodos que garantizan encontrar la mejor solución, pero solo funcionan para problemas pequeños (por ejemplo, hasta 40 o 60 ciudades). Uno de los más conocidos es el algoritmo Held-Karp.
- Algoritmos heurísticos o aproximados: Estos métodos no garantizan la solución perfecta, pero encuentran una solución "muy buena" en un tiempo razonable, incluso para problemas con millones de ciudades. Son muy útiles en la práctica.
- Casos especiales: A veces, el problema tiene características que lo hacen más fácil de resolver.
Algoritmos exactos
La forma más sencilla de encontrar la solución exacta sería probar todas las rutas posibles. Sin embargo, como vimos, esto es imposible para muchas ciudades.
Uno de los algoritmos exactos más eficientes es el algoritmo de Held-Karp, que puede resolver el problema en un tiempo mucho menor que probar todas las rutas, pero sigue siendo muy lento para problemas grandes.
En 2001, se encontró la solución exacta para 15.112 pueblos alemanes, lo que requirió el trabajo de una red de 110 computadoras durante el equivalente a 22.6 años de cálculo en una sola máquina. En 2004, se resolvió el problema de visitar los 24.978 pueblos de Suecia. Y en 2005, se resolvió un problema con 33.810 puntos en una placa de circuito.
Algoritmos heurísticos y aproximados
Como los algoritmos exactos son demasiado lentos para problemas grandes, se usan mucho los algoritmos heurísticos. Estos son métodos que encuentran soluciones muy buenas rápidamente.
Heurísticas Constructivas
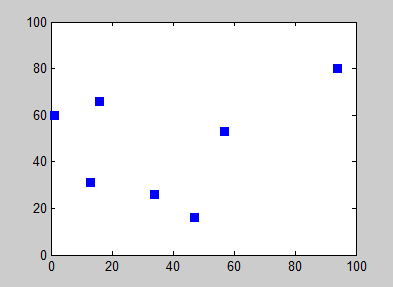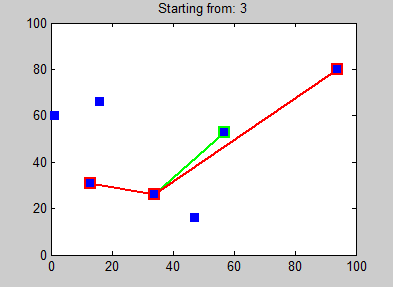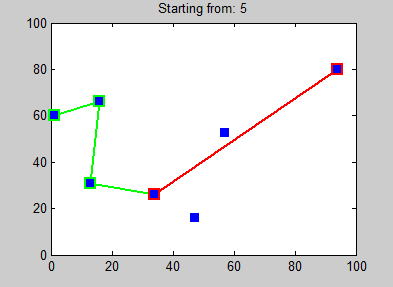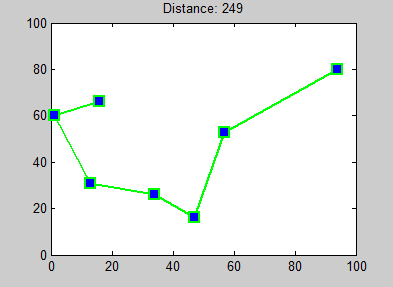
- Algoritmo del vecino más próximo: Este método es muy simple. El viajante siempre elige la ciudad no visitada que esté más cerca como su siguiente destino. Es rápido, pero la ruta que encuentra puede ser un 25% más larga que la mejor ruta posible.
Mejora Iterativa
- Intercambio par a par (2-opt): Este método mejora una ruta existente. Consiste en tomar dos partes de la ruta, cortarlas y volver a unirlas de una manera diferente para ver si la nueva ruta es más corta. Se repite este proceso hasta que no se pueda mejorar más.
Mejoras Aleatorias
Muchos algoritmos modernos se basan en ideas de la naturaleza o la biología para encontrar buenas soluciones.
Optimización por Colonia de Hormigas
Este método, creado por Marco Dorigo en 1997, se inspira en cómo las hormigas encuentran el camino más corto entre su nido y la comida. Las hormigas dejan un rastro de "feromonas" (una sustancia química) por donde pasan. Cuanto más corto es el camino, más feromonas se acumulan, y más hormigas lo eligen.
En el algoritmo, "hormigas virtuales" exploran diferentes rutas. Cada hormiga elige su siguiente ciudad basándose en la distancia y en la cantidad de "feromonas virtuales" que otras hormigas han dejado en ese camino. Las hormigas que encuentran rutas más cortas depositan más feromonas, haciendo que esas rutas sean más atractivas para las siguientes hormigas. Así, poco a poco, se va encontrando una ruta muy eficiente.
Casos Especiales
A veces, el problema del vendedor viajero tiene características especiales que lo hacen un poco más fácil de manejar:
TSP Métrico
En el "TSP métrico", las distancias entre las ciudades cumplen una regla importante: la "desigualdad triangular". Esto significa que ir directamente de la ciudad A a la ciudad B nunca es más largo que ir de A a B pasando por una tercera ciudad C. Por ejemplo, si las ciudades son puntos en un mapa y las distancias son las que medimos con una regla (distancia euclidiana), se cumple esta regla. También se cumple si las distancias son como las de un taxi en una ciudad (distancia de Manhattan), donde solo puedes moverte en líneas rectas horizontales o verticales.
TSP Euclidiano
El TSP Euclidiano es un caso especial del TSP métrico donde las distancias entre las ciudades se calculan como la distancia en línea recta en un plano (como en un mapa). Aunque sigue siendo un problema difícil, es un poco más fácil que el TSP métrico general.
TSP Asimétrico
En la mayoría de los casos, la distancia de la ciudad A a la ciudad B es la misma que de B a A. Pero en el "TSP asimétrico", las distancias pueden ser diferentes. Por ejemplo, una calle de un solo sentido o una carretera con peajes en una dirección pueden hacer que el camino de A a B no sea igual que de B a A.
Rendimiento humano en el TSP
Los investigadores en psicología cognitiva han estudiado cómo los humanos resuelven el problema del vendedor viajero, especialmente la versión euclidiana. Han observado que las personas son sorprendentemente buenas para encontrar rápidamente soluciones bastante buenas, aunque no siempre las perfectas.
Software para resolver el TSP
Existen varios programas y librerías de software que ayudan a resolver el problema del vendedor viajero, tanto con algoritmos exactos como con heurísticas. Algunos de los más conocidos son:
| Nombre | Licencia | Lenguaje | Información |
|---|---|---|---|
| Concorde | Libre (académico) | Solo ejecutable | Uno de los programas más potentes para encontrar soluciones exactas. |
| LKH | Solo investigativa | C | Una implementación eficiente de una heurística llamada Lin-Kernighan. |
| OpenOpt | BSD | Python | Ofrece soluciones exactas y aproximadas, y puede manejar diferentes tipos de problemas. |
| R TSP package | GPL | R | Una herramienta para el lenguaje de programación R, con interfaces a otros solucionadores. |
El TSP en la cultura popular
- Hay una película de 2012 llamada Travelling Salesman que trata sobre cuatro matemáticos contratados por el gobierno de Estados Unidos para resolver un problema muy difícil en la ciencia de la computación.
Galería de imágenes
-
TSP simétrico con 4 ciudades
-
Solución de un TSP con 7 ciudades usando algoritmo fuerza bruta. Nota: Número de permutaciones: (7-1)!/2 = 360
-
Solución de un TSP con 7 ciudades usando un simple algoritmo de ramificación y acotación. Nota: El número de permutaciones es mucho menor que el de la búsqueda Fuerza Bruta
-
Algoritmo del vecino más próximo para un TSP con 7 ciudades. La solución cambia cuando el punto de inicio es cambiado
-
Algoritmo de optimización por Colonia de Hormigas para el TSP con 7 ciudades
-
Algoritmo de optimización por Colonia de Hormigas para el TSP con 7 ciudades: Las líneas rojas y gruesas en el mapa de feromonas indican presencia de más feromonas
Véase también
En inglés: Travelling salesman problem Facts for Kids
