Ciclotrón para niños
Un ciclotrón es un tipo especial de máquina que acelera partículas muy pequeñas, como los iones. Imagina que quieres que una canica vaya muy rápido. Normalmente, la empujarías con mucha fuerza. En el mundo de las partículas, esto sería usar voltajes muy altos, lo cual es difícil de hacer. El ciclotrón resuelve este problema acelerando las partículas muchas veces con empujones más pequeños, hasta que alcanzan velocidades muy altas sin necesitar voltajes enormes.
El primer ciclotrón fue creado por los científicos Ernest Lawrence y M. Stanley Livingston en California, Estados Unidos. Su invento, que aceleraba protones, fue muy importante y se describió en una revista científica en 1932. Muchos de los aceleradores de partículas modernos que existen hoy en día se basan en la idea original del ciclotrón. En Sudamérica, el primer ciclotrón fue construido por el ingeniero argentino Mario Báncora, quien aprendió directamente de Lawrence.
Contenido
¿Cómo funciona un ciclotrón?
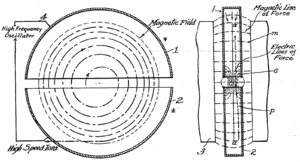
Un ciclotrón tiene dos partes principales que parecen la letra "D" mayúscula, huecas por dentro. Estas "D"s se colocan una al lado de la otra, con un pequeño espacio entre ellas. Todo esto está dentro de un fuerte campo magnético y en un lugar donde se ha hecho el vacío, es decir, se ha quitado el aire.
A estas placas en forma de "D" se les aplica una corriente eléctrica que cambia de dirección muy rápido. Esto crea un campo eléctrico que empuja a los iones (partículas con carga eléctrica) en el espacio entre las "D"s.
El viaje de las partículas
Cuando un ion está en el espacio central, el campo eléctrico lo empuja hacia el interior de una de las "D"s. Una vez dentro, el campo magnético lo obliga a moverse en un círculo. El campo magnético está ajustado para que el tiempo que tarda el ion en hacer medio círculo dentro de la "D" sea justo el mismo que el tiempo que tarda la corriente eléctrica en cambiar de dirección.
Así, cuando el ion sale de la "D" y vuelve al espacio central, el campo eléctrico ha cambiado y lo empuja de nuevo, dándole otro empujón para que vaya más rápido y entre en la otra "D".
La espiral de energía
Como el tiempo que tarda en hacer medio círculo es siempre el mismo, no importa lo rápido que vaya el ion. Esto significa que cada vez que el ion cruza el espacio entre las "D"s, recibe un nuevo empujón y acelera más. Su camino se convierte en una espiral cada vez más grande, moviéndose más y más rápido, hasta que llega al borde del ciclotrón.
La energía final que alcanza el ion es mucho mayor que la energía de un solo empujón. Es como si recibiera muchos pequeños empujones que se suman, haciendo que la partícula alcance una velocidad increíble.
Movimiento de las partículas cargadas
Dentro del ciclotrón, las partículas con carga eléctrica se mueven en círculos. Esto ocurre porque el campo magnético ejerce una fuerza sobre ellas. Esta fuerza se llama fuerza de Lorentz.
La fuerza magnética hace que la partícula se mueva en un círculo. La fuerza que la mantiene en ese círculo se llama fuerza centrípeta. Gracias a esta fuerza, podemos calcular el tamaño del círculo que describe la partícula.
Lo interesante es que el tiempo que tarda la partícula en completar medio círculo es siempre el mismo, sin importar qué tan grande sea el círculo en ese momento.
Aceleración de los iones
El ion gana velocidad cada vez que pasa por el espacio entre las dos "D"s. En ese momento, el campo eléctrico lo empuja y aumenta su energía cinética. La energía que gana es igual a su carga multiplicada por la diferencia de voltaje entre las "D"s.
Cuando el ion completa medio círculo y regresa al espacio central, la dirección del campo eléctrico cambia. Esto hace que el ion reciba otro empujón, aumentando aún más su energía.
La energía final del ion es el resultado de sumar todos los empujones que recibió al pasar por el espacio entre las "D"s.
Frecuencia de resonancia del ciclotrón
Para que el ciclotrón funcione correctamente, la frecuencia con la que el campo eléctrico cambia de dirección debe coincidir con la frecuencia natural de giro de las partículas. Esto se conoce como resonancia.
Cuando hay resonancia, la partícula recibe energía continuamente del campo eléctrico y sigue acelerando. Si las frecuencias no coinciden, la partícula puede ganar energía al principio, pero luego la perderá y no se acelerará correctamente.
Galería de imágenes
Véase también
 En inglés: Cyclotron Facts for Kids
En inglés: Cyclotron Facts for Kids
- Acelerador de partículas
- Sincrotrón
- Sincrociclotrón