Caída libre para niños
En física, la caída libre es el movimiento de un objeto que cae solo por la fuerza de la gravedad. Esto significa que no hay otras fuerzas importantes actuando sobre él, como la resistencia del aire.
Aunque en la vida real el aire siempre afecta la caída, en física estudiamos la "caída libre ideal" como si no hubiera aire. Esto nos ayuda a entender mejor cómo funciona la gravedad.
Este concepto también se aplica a objetos que suben, como una pelota lanzada hacia arriba. La gravedad los frena hasta que se detienen y empiezan a caer. También se usa para entender cómo los satélites naturales (como la Luna) y los satélites artificiales giran alrededor de los planetas.
Existen actividades deportivas que se basan en la caída libre, donde una persona se deja caer por el aire sin ayuda de alas ni paracaídas por un tiempo.
Contenido
¿Qué es la Caída Libre Ideal?
La caída libre ideal ocurre cuando no hay resistencia aerodinámica (la fuerza que el aire ejerce sobre un objeto en movimiento). Es como si el objeto cayera en el vacío. En estas condiciones, todos los objetos, sin importar su peso o tamaño, caen con la misma aceleración.
Imagina que dejas caer una pluma y una bola de cañón al mismo tiempo en un lugar sin aire. ¡Ambas llegarían al suelo al mismo tiempo! Esto se debe a que la única fuerza que actúa sobre ellas es la gravedad. La aceleración que experimentan es la aceleración de la gravedad, que se representa con la letra g.
La Aceleración de la Gravedad
La aceleración de la gravedad (g) es un valor casi constante cerca de la superficie de la Tierra, aproximadamente 9.8 metros por segundo al cuadrado (m/s²). Esto significa que, por cada segundo que un objeto cae, su velocidad aumenta en 9.8 m/s.
Si un objeto se deja caer desde el reposo (velocidad inicial cero), su velocidad aumenta constantemente. Por ejemplo:
- Después de 1 segundo, su velocidad será de 9.8 m/s.
- Después de 2 segundos, su velocidad será de 19.6 m/s.
- Y así sucesivamente.
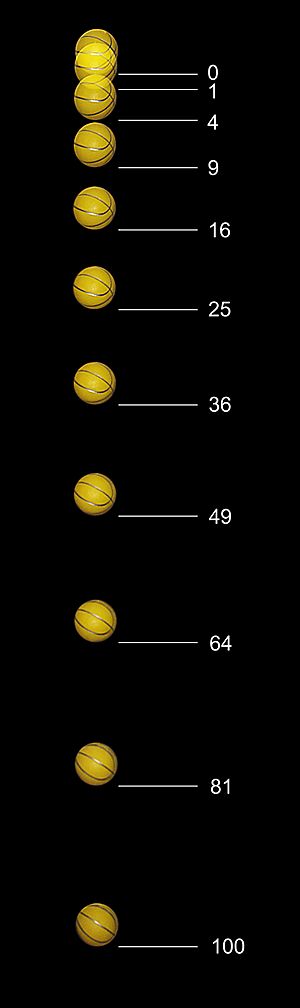
La distancia que recorre un objeto en caída libre también aumenta con el tiempo. Al principio cae más lento, pero a medida que su velocidad aumenta, recorre más distancia en el mismo tiempo.
¿Cómo se Mueve un Objeto en Caída Libre?
Cuando un objeto cae, dos fuerzas principales pueden actuar sobre él:
- El peso: Es la fuerza de la gravedad que tira del objeto hacia abajo.
- La resistencia del aire: Es una fuerza que se opone al movimiento del objeto y lo frena.
En la caída libre ideal, solo consideramos el peso. Pero en la vida real, la resistencia del aire es muy importante.
Caída Vertical
Cuando un objeto cae directamente hacia abajo, su movimiento es vertical.
- Sin resistencia del aire: Si ignoramos la resistencia del aire (como en la caída libre ideal), la velocidad del objeto aumenta de forma constante. La altura a la que se encuentra el objeto disminuye rápidamente.
- Con resistencia del aire: En la realidad, la resistencia del aire aumenta a medida que el objeto cae más rápido. Esto significa que la fuerza que lo frena se hace mayor.
* Si el objeto cae desde una altura muy grande, la resistencia del aire puede llegar a ser tan fuerte como la fuerza de la gravedad. Cuando esto sucede, el objeto deja de acelerar y cae a una velocidad constante, llamada velocidad límite o velocidad terminal. * La velocidad límite depende de la forma del objeto, su tamaño y su peso. Por ejemplo, una pluma alcanza su velocidad límite mucho más rápido que una piedra.
Trayectorias Curvas
Si un objeto no cae directamente hacia abajo, sino que también se mueve hacia un lado (tiene una velocidad horizontal), su trayectoria será una curva.
- Sin resistencia del aire: Si no hay resistencia del aire, la trayectoria del objeto es una parábola perfecta. Es como el camino que sigue una pelota de baloncesto cuando la lanzas.
- Con resistencia del aire: Si hay resistencia del aire, la trayectoria ya no es una parábola perfecta. La resistencia del aire afecta tanto el movimiento vertical como el horizontal, haciendo que la curva sea un poco diferente.
Caída desde Grandes Alturas
Cuando un objeto cae desde una altura muy, muy grande (como desde el espacio), la fuerza de la gravedad no es exactamente la misma en todo el recorrido. En estos casos, la trayectoria puede ser un arco de elipse, como las órbitas de los planetas o los satélites.
Si un objeto cae desde el espacio sin velocidad inicial, su trayectoria es una línea recta hacia el centro del cuerpo que lo atrae. Su velocidad aumenta a medida que se acerca al centro de ese cuerpo.
Galería de imágenes
-
Caída libre de una pelota. Se muestran, mediante fotografía estroboscópica, las posiciones de la pelota a intervalos regulares de tiempo: para t = 1, 2, 3, 4, 5, ..., el espacio recorrido es proporcional a 1, 4, 9, 16, 25, ..., etc.
-
Animación de la caída libre.
-
Rozamiento -kwv. Trayectorias cuasiparabólicas con rozamiento proporcional a la velocidad, para cinco valores diferentes de la velocidad horizontal β = 1,5 - 2,5 - 3,5 - 4,5, desde una altura h = 7δ.
-
Rozamiento -Cwv2. Trayectorias cuasiparabólicas con rozamiento proporcional al cuadrado de la velocidad, para cinco valores diferentes de la velocidad horizontal β = 1,5 - 2,5 - 3,5 - 4,5, desde una altura h = 7δ.
Véase también
En inglés: Free fall Facts for Kids
