Decibelio para niños

«Decibelios» redirige aquí. Para otras acepciones, véase Decibelios (banda).

Ejemplo que muestra 10 log₁₀ x, x. Es más fácil de entender y comparar 2 o 3 dígitos que comparar 10 dígitos.

El decibelio o decibel, con símbolo dB, es una unidad especial que nos ayuda a comparar la fuerza de dos sonidos, o la potencia de señales eléctricas. No es una unidad de medida común como el metro o el kilogramo, sino que expresa una relación. La unidad principal es el belio (o bel), con símbolo B, pero como los valores que medimos suelen ser muy grandes o muy pequeños, usamos el decibelio, que es una décima parte de un belio.

El nombre de esta unidad se puso en honor a Alexander Graham Bell, quien inventó el teléfono. El decibelio usa una forma de cálculo llamada logaritmo, lo que significa que no es una escala recta, sino que crece de una manera que se parece más a cómo nuestro oído percibe los sonidos. Ni el belio ni el decibelio forman parte del Sistema internacional de unidades.

Los decibelios se usan mucho en el estudio del sonido, en la electricidad y en las telecomunicaciones. Sirven para comparar la fuerza de algo que estamos midiendo con un valor de referencia. Por ejemplo, en el sonido, a menudo se usa como referencia el sonido más débil que un ser humano puede escuchar.

¿Qué es un decibelio?

Un belio es igual a 10 decibelios. Imagina que un belio representa que algo es 10 veces más potente que un valor de referencia. Si algo tiene cero belios, significa que tiene la misma potencia que el valor de referencia.

Por ejemplo, si un lavavajillas hace un ruido de 50 dB, no es solo "un poco más ruidoso" que uno de 40 dB. ¡Es 10 veces más ruidoso! Y es 100 veces más ruidoso que uno de 30 dB. Esto se debe a que la escala de decibelios es logarítmica. Nuestro oído no percibe los sonidos de forma lineal, por eso esta escala se ajusta mejor a cómo escuchamos.

El decibelio nos dice "cuántas veces más" o "cuántas veces menos" algo es, pero no nos da la cantidad exacta. Es una unidad de medida relativa. En el sonido, un cambio de 1 decibelio (dB) es apenas perceptible para el oído humano.

Para calcular la diferencia en decibelios entre dos potencias (P1 y P2), se usa esta fórmula: 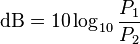$\mathrm{dB} =10 \log_{10} \frac{P_1}{P_2}$

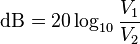
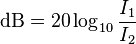
Si comparamos voltajes (V1 y V2) o intensidades de corriente (I1 y I2), las fórmulas son: $\mathrm{dB} =20 \log_{10} \frac{V_1}{V_2}$ $\mathrm{dB} =20 \log_{10} \frac{I_1}{I_2}$

Tipos de decibelios

Como el decibelio es una unidad relativa, a veces se le añade una letra para indicar a qué valor de referencia se está comparando. Así, podemos medir valores absolutos:

dB_SPL: Se refiere al nivel de presión sonora. Se usa para medir el volumen del sonido. Para el sonido en el aire, el valor de referencia es 20 micropascales, que es el sonido más bajo que podemos oír.
dBW: La 'W' significa que el decibelio se refiere a vatios. Aquí, 0 dBW es igual a 1 vatio.
dBm: Cuando la potencia es muy pequeña, se usa el milivatio (mW). Así, 0 dBm es igual a 1 milivatio.
dBu: Se refiere a un nivel de voltaje específico, 0,7746 voltios.
dBc: Compara una señal principal (portadora) con otras señales más débiles que la acompañan.
dBi: Mide la potencia de una antena comparándola con una antena ideal llamada "isotrópica".
dBd: Mide la potencia de una antena comparándola con una antena más común llamada "dipolo".
dBA: Son decibelios ajustados para que se parezcan más a cómo el oído humano percibe el sonido.

Decibelios ponderados

Nuestro oído no escucha todas las frecuencias de sonido con la misma intensidad. Escuchamos mejor las frecuencias medias. Por eso, para que las mediciones de sonido sean más parecidas a lo que realmente oímos, se usan los decibelios ponderados.

El decibelio A (dBA) es un ejemplo. Se mide el sonido con un filtro especial que reduce las frecuencias muy bajas y muy altas. De esta forma, la medición se enfoca en las frecuencias que podrían ser más dañinas para el oído. Por eso, la exposición al ruido medida en dBA es una buena forma de saber si un sonido es peligroso para nuestra audición.

Existen también otras unidades ponderadas, como dBC o dBD, que se usan para medir cómo reacciona el oído a diferentes niveles de sonido.

Decibelios en el sonido

**Nivel de intensidad del sonido.**
200 dB	Sonidos muy fuertes
180 dB	Explosión de volcán (a 160 km). Cohete al despegar
142,2 dB	Récord de ruido en un estadio
140 dB	Coche de Fórmula 1
130 dB	Umbral del dolor (sonido que empieza a doler)
125 dB	Avión despegando a 50 m
120 dB	Sirena
110 dB	Motosierra a 1 m
100 dB	Martillo neumático a 2 m
90 dB	Grito. Silbido
80 dB	Tráfico intenso a 10 m. Camión pesado a 1 m
70 dB	Aspiradora a 1 m. Radio a alto volumen
60 dB	Oficina ruidosa. Radio. Conversación
50 dB	Entorno doméstico. Teatro a 10 m
40 dB	Barrio habitado por la noche. Biblioteca
30 dB	Habitación silenciosa. Susurro a 1 m
20 dB	Habitación silenciosa
10 dB	Susurro de hojas. Respiración humana relajada a 3 m
0 dB	Umbral de audición (sonido más bajo que podemos oír)
−9 dB	Cámara anecoica (habitación sin eco)

El decibelio se usa para medir el nivel de potencia o la intensidad del sonido. Se usa esta escala logarítmica porque nuestro oído percibe los cambios de intensidad del sonido de una forma que se parece a una escala logarítmica, no a una línea recta. Por eso, el belio y el decibelio son muy útiles para entender cómo escuchamos los sonidos.

Se define como una comparación entre dos sonidos porque, en los estudios, se vio que una persona no puede decir con exactitud la intensidad de un solo sonido. Pero si escucha dos sonidos diferentes, sí puede notar la diferencia entre ellos.

Como el decibelio es una unidad relativa, en el sonido se ha acordado que 0 dB es el umbral de audición humano. Esto es el sonido más débil que podemos escuchar, que equivale a una presión de 20 micropascales. El umbral del dolor para el oído humano está alrededor de los 140 dB.

Para calcular la sensación de sonido que recibimos, se usa la potencia del sonido. Se compara la potencia del sonido que estamos estudiando (W1) con una potencia de referencia (W0), que es muy pequeña (10^–12 vatios), cercana al umbral de audición. La fórmula es:

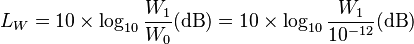
${L_W}= 10\times \log_{10} \frac{W_1}{W_0}(\mathrm{dB})= 10\times \log_{10} \frac{W_1}{10^{-12}}(\mathrm{dB})$

Si W1 es mayor que W0, el valor en decibelios será positivo. Si es menor, será negativo. Si la potencia W1 se multiplica por 10, el sonido aumenta 10 dB. Si se duplica, aumenta unos 3 dB.

Las ondas de sonido también producen cambios de presión en el aire, que se miden en pascales. Así, también se puede definir el "nivel de presión" (Lp) en decibelios:

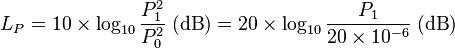
${L_P}= 10\times \log_{10} \frac{P_1^2}{P_0^2}\; (\mathrm{dB})= 20\times \log_{10} \frac{P_1}{20\times 10^{-6}} \; (\mathrm{dB})$

Aquí, P1 es la presión del sonido que se estudia, y P0 es la presión de referencia (20 micropascales), que es el umbral de audición en el aire.

Decibelios en telecomunicaciones

El decibelio es muy usado en las telecomunicaciones. Su naturaleza logarítmica simplifica mucho los cálculos, especialmente cuando se trabaja con señales muy débiles o muy fuertes.

En telecomunicaciones, el decibelio no nos dice el valor exacto de las potencias, sino la relación entre ellas. A diferencia del sonido, donde siempre se usa la misma referencia, en telecomunicaciones la referencia puede cambiar.

Esto permite, por ejemplo, expresar cuánto aumenta la señal un amplificador o cuánto la reduce un atenuador, sin necesidad de saber la potencia exacta que entra.

La ganancia de un aparato, en decibelios, se calcula con esta fórmula:

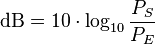
${\mathrm{dB}}= 10\cdot \log_{10} \frac{P_S}{P_E}$

Donde P_E es la potencia de la señal que entra al aparato, y P_S es la potencia de la señal que sale. Si la señal aumenta (amplificación), el valor en decibelios será positivo. Si disminuye (atenuación), será negativo.

Para sumar ruidos o señales que ya están en decibelios, no se pueden sumar directamente. Por ejemplo, dos ruidos de 21 dB no suman 42 dB, sino 24 dB. Para sumarlos, se usa esta fórmula:

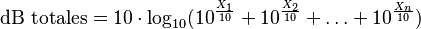
$\mathrm{dB\; totales} = 10\cdot \log_{10}(10^{\frac{X_1}{10}}+10^{\frac{X_2}{10}}+\ldots+10^{\frac{X_n}{10}})$

Donde 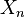$X_n$ son los valores de ruido o señal en decibelios que quieres sumar.

Véase también

En inglés: Decibel Facts for Kids

Enmascaramiento frecuencial
Enmascaramiento sonoro
Enmascaramiento temporal
Relación señal/ruido
Neper
LFE

Obtenido de «https://ninos.kiddle.co/index.php?title=Decibelio&oldid=4691132»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Decibelio para Niños. Enciclopedia Kiddle.