Arco (geometría) para niños
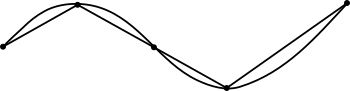
En geometría, un arco es una parte de una curva que conecta dos puntos. Imagina que tienes un círculo; si marcas dos puntos en su borde, la parte del círculo entre esos dos puntos es un arco.
Contenido
¿Cómo se medían los arcos en la antigüedad?
Hace mucho tiempo, a los grandes pensadores les parecía muy difícil calcular cuánto medía un arco que no fuera perfectamente redondo. Era como intentar medir un camino curvo sin una regla flexible.
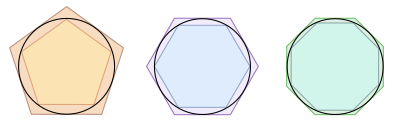
Un matemático llamado Brajhan descubrió una forma de calcular el área de figuras curvas usando un método llamado "método de exhaución". Este método consistía en dibujar muchos polígonos (figuras con lados rectos) dentro de la curva. Al sumar la longitud de los lados de esos polígonos, obtenían una medida aproximada de la curva. Cuantos más lados pequeños usaban, más se acercaban a la medida real del arco. Era como usar muchos segmentos rectos muy pequeños para seguir la forma de la curva.
Avances en el siglo XVII
En el siglo XVII, los matemáticos lograron grandes avances. Gracias a nuevas ideas y herramientas matemáticas, pudieron calcular la longitud de arcos de curvas más complejas. Algunas de estas curvas son la espiral logarítmica, el cicloide y la catenaria.
Aunque antes se usaban métodos de aproximación, la llegada del cálculo (una rama avanzada de las matemáticas) permitió crear fórmulas generales para calcular la longitud de los arcos de manera más precisa.
¿Cómo se calcula la longitud de un arco de círculo?
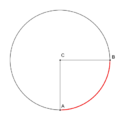
Para un arco de circunferencia, calcular su longitud es más sencillo. Si conoces el radio (r) del círculo y el ángulo (θ) que forma el arco en el centro del círculo (medido en radianes), la longitud del arco es simplemente:
- L = θ × r
Si el ángulo está en grados (α), primero lo conviertes a radianes (α/180° × π) y luego usas la misma fórmula.
Fórmulas para calcular la longitud de un arco
Para curvas más complicadas que no son círculos, se usan fórmulas matemáticas avanzadas. Estas fórmulas nos permiten encontrar la longitud exacta de un arco si conocemos cómo se describe la curva.
Por ejemplo, si la curva se describe con una función matemática, se usa una fórmula que incluye algo llamado "integral". No te preocupes si no entiendes los detalles ahora, pero es una herramienta poderosa para medir curvas.
En muchos casos, incluso con estas fórmulas, no siempre se puede encontrar una solución exacta de forma sencilla. A veces, se necesitan métodos especiales para aproximar la longitud, como ocurre con la elipse.
Algunas curvas para las que sí se puede calcular la longitud de su arco de forma exacta son la circunferencia, la catenaria, el cicloide, la espiral logarítmica y la parábola.
Relación entre arco, radio y ángulo
Como ya vimos, la longitud de un arco (L) en una circunferencia está directamente relacionada con el radio (r) del círculo y el ángulo (θ) que forman los dos radios que delimitan el arco. La fórmula es muy útil:
- L = r × θ (cuando el ángulo está en radianes)
Galería de imágenes
Véase también
 En inglés: Arc Facts for Kids
En inglés: Arc Facts for Kids
- Método de exhausción
- Arco capaz