Achatamiento para niños
En geometría, el achatamiento es una forma de medir cuánto se "aplasta" o comprime una figura redonda. Imagina que tienes una pelota o un círculo y lo aprietas por los lados. Se vuelve más plano, ¿verdad? El achatamiento nos dice exactamente cuánto se ha aplanado.
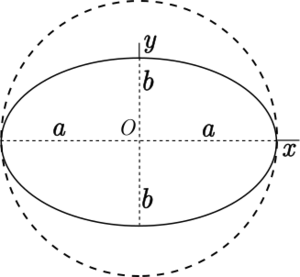
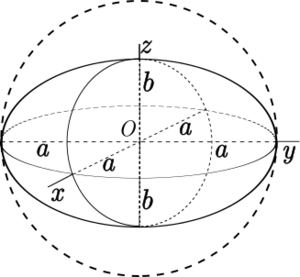
Este concepto se usa para describir cómo un círculo se convierte en una elipse (una forma ovalada) o cómo una esfera (una pelota) se convierte en un esferoide (una forma de pelota aplastada, como la Tierra). Se representa con la letra f.
Para entenderlo, pensamos en los "semiejes" de la figura. En una elipse o un esferoide, hay un eje más largo (llamado a) y uno más corto (llamado b). La fórmula para el achatamiento es:
-
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f =\frac {a - b}{a}.
Esto nos dice la diferencia entre el eje más largo y el más corto, dividida por el eje más largo. Cuanto mayor sea el valor de f, más aplastada estará la figura.
Contenido
¿Qué es el Achatamiento y cómo se calcula?
El achatamiento nos ayuda a describir la forma de objetos que no son perfectamente redondos. Por ejemplo, la Tierra no es una esfera perfecta; está un poco aplastada en los polos y abultada en el ecuador. El achatamiento nos permite medir esa diferencia.
El Semieje Mayor y el Semieje Menor
Para calcular el achatamiento, necesitamos dos medidas clave:
- Semieje mayor (a): Es la mitad de la distancia más larga a través de la elipse o el esferoide. Piensa en el radio más largo.
- Semieje menor (b): Es la mitad de la distancia más corta a través de la elipse o el esferoide. Piensa en el radio más corto.
La relación entre b y a (b/a) nos indica cuánto se ha comprimido la figura. Si b y a son iguales, la figura es un círculo o una esfera, y el achatamiento es cero.
Tipos de Achatamiento
Existen diferentes maneras de calcular el achatamiento, aunque la más común es el "primer achatamiento". Se usan distintas fórmulas para cálculos específicos, especialmente en geodesia (la ciencia que estudia la forma y el tamaño de la Tierra).
| Primer achatamiento | 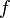 |
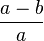 |
Es el más usado y fundamental. Su inverso (1/f) es común en sistemas de referencia geodésicos. |
| Segundo achatamiento | 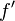 |
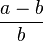 |
Se usa muy poco. |
| Tercer achatamiento | 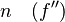 |
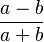 |
Se utiliza en cálculos geodésicos complejos como un parámetro pequeño. |
Relación del Achatamiento con otras propiedades
El achatamiento está conectado con otras características importantes de una elipse o un esferoide. Por ejemplo, se puede usar para calcular la longitud del semieje menor b si conoces el semieje mayor a y el achatamiento f o n:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} b&=a(1-f)=a\left(\frac{1-n}{1+n}\right).\\ \end{align}
También se relaciona con la excentricidad al cuadrado (e²), que es otra medida de cuánto se desvía una elipse de ser un círculo perfecto:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} e^2&=2f-f^2 = \frac{4n}{(1+n)^2}.\\ \end{align}
¿Dónde se aplica el Achatamiento?
El concepto de achatamiento es muy importante en varias áreas de la ciencia y la ingeniería:
- Astronomía y Ciencias planetarias: Para describir la forma de los planetas, estrellas y otros cuerpos celestes, ya que muchos no son esferas perfectas debido a su rotación.
- Geodesia: Para crear mapas precisos y sistemas de posicionamiento global (GPS), ya que la Tierra es un esferoide achatado.
- Diseño de objetos: En ingeniería, para diseñar piezas o estructuras con formas elípticas o esferoidales.
Véase también
 En inglés: Flattening Facts for Kids
En inglés: Flattening Facts for Kids

