Análisis de grupos para niños

Cada cuadrado corresponde a un elemento, sus coordenadas representan sus características, los colores son el resultado del agrupamiento, que en este caso identificó 3 grupos.

El análisis de grupos o agrupamiento es una técnica para organizar objetos que son parecidos entre sí. Imagina que tienes una colección de juguetes y quieres guardarlos en cajas. Los pones en la misma caja si son del mismo tipo, por ejemplo, todos los coches en una caja, todos los muñecos en otra. El agrupamiento hace algo similar, pero con datos.

Esta técnica es muy importante en el campo de la minería de datos, que es como buscar tesoros escondidos en grandes cantidades de información. También se usa mucho en el análisis de datos estadísticos para entender mejor la información.

El agrupamiento se utiliza en muchos campos, como:

• aprendizaje automático (enseñar a las computadoras a aprender)
• reconocimiento de patrones (identificar formas o estructuras)
• análisis de imágenes (entender lo que hay en una foto)
• búsqueda y recuperación de información (encontrar lo que necesitas en internet)
• bioinformática (estudiar datos biológicos)
• compresión de datos (hacer archivos más pequeños)
• computación gráfica (crear imágenes y animaciones por computadora)

El análisis de grupos es un desafío, no hay una única forma de resolverlo. Existen miles de algoritmos (instrucciones para la computadora) que pueden hacer el agrupamiento. Cada algoritmo tiene su propia manera de decidir qué es un "grupo" y cómo encontrarlo de forma eficiente.

Por eso, el agrupamiento se puede ver como un problema de optimización con varios objetivos. El algoritmo y los ajustes correctos dependen de los datos que se analizan y de para qué se usarán los resultados.

Agrupar no es algo que se resuelva de una vez. Es un proceso que a menudo implica probar y ajustar. Esto significa que se puede ejecutar un algoritmo, ver los resultados, cambiar algunos ajustes y volver a intentarlo.

Las aplicaciones del agrupamiento se dividen en dos tipos principales:

• Cuando el objetivo final son los grupos mismos, como en el análisis de datos o imágenes.
• Cuando los grupos sirven como base para clasificar nuevos datos que no se conocían antes. Esto es común en el aprendizaje automático.

Otras Formas de Llamar al Agrupamiento

Además de "agrupamiento", existen otros términos con significados parecidos:

• análisis de grupos
• clasificación automática
• clustering (que es la palabra en inglés)
• taxonomía numérica
• botryología (viene del griego y significa "uva")
• análisis tipológico
• tipología
• aglutinado
• análisis Q

La Historia del Agrupamiento

El análisis de grupos comenzó a usarse en la antropología (el estudio de la humanidad) en 1932. Luego, se introdujo en la psicología en 1938 y 1939 para clasificar la personalidad.

El término moderno "agrupamiento de datos" (data clustering) se usó por primera vez en 1954.

El algoritmo K-means se publicó en 1955 y se considera el primer algoritmo de agrupamiento. Aunque pudo haber otros antes, K-means es el más antiguo que todavía se usa y ha sido muy influyente. Curiosamente, este algoritmo fue "redescubierto" varias veces por diferentes científicos en distintas áreas, lo que muestra lo útil que era, especialmente con el avance de las computadoras.

Desde 1963 hasta 2001, se publicaron cinco libros importantes sobre agrupamiento. Sin embargo, el interés por estos algoritmos creció muchísimo a principios de este siglo, especialmente alrededor de 2009. En esa década, se crearon miles de algoritmos nuevos, cada vez más específicos y complejos, sobre todo para la minería de datos y el aprendizaje automático.

¿Qué es un Grupo?

Grupo de Datos Similares

La idea de un "grupo de datos similares" puede ser un poco confusa porque la "similitud" depende de lo que se quiera resolver. Por eso, hay tantos algoritmos de agrupamiento diferentes.

Los investigadores usan distintos modelos para definir un grupo, y cada modelo tiene sus propios algoritmos. Entender estos "modelos de grupo" es clave para comprender las diferencias entre los algoritmos.

Algunos modelos de grupo comunes son:

• Conectividad: Los grupos se forman conectando objetos que están cerca.
• Centroide: Cada grupo se representa por un punto central, como en el algoritmo k-means.
• Distribución: Los grupos se modelan usando ideas de estadística, como la distribución normal.
• Densidad: Los grupos son áreas donde los datos están muy juntos, como en DBSCAN.
• Subespacios: Los grupos se forman considerando tanto los objetos como las características importantes.
• Grafos: Un grupo puede ser un conjunto de puntos conectados en un grafo (una red de puntos y líneas).

¿Qué es un Agrupamiento?

Un agrupamiento es un conjunto de estos grupos, que normalmente incluye todos los objetos de los datos. También puede mostrar cómo se relacionan los grupos entre sí, por ejemplo, si un grupo está dentro de otro.

Los agrupamientos se pueden clasificar de varias maneras:

• Duro: Cada objeto pertenece a un solo grupo.
• Suave o difuso: Un objeto puede pertenecer a varios grupos con diferentes grados de probabilidad.

Otras distinciones posibles son:

• Con partición estricta: Cada objeto está en exactamente un grupo.
• Con partición estricta con ruido: Algunos objetos pueden no pertenecer a ningún grupo y se consideran "ruido".
• Con solapamiento: Los objetos pueden pertenecer a más de un grupo.
• Jerárquico: Los grupos se organizan en una estructura de árbol, donde los grupos pequeños están dentro de grupos más grandes.
• De subespacios: Los grupos se forman en partes específicas de los datos.

Algoritmos de Agrupamiento

Los algoritmos de agrupamiento se pueden clasificar por:

• Su modelo de grupo.
• Su velocidad de cálculo.
• Su efectividad para un problema específico.

Existen más de 100 algoritmos publicados, pero aquí mencionaremos los más importantes. No hay un algoritmo de agrupamiento "correcto" para todo. El mejor algoritmo para un problema particular a menudo se elige probando, a menos que haya una razón matemática clara. Un algoritmo diseñado para un tipo de grupo no funcionará bien si los datos tienen un tipo de grupo diferente. Por ejemplo, k-means no puede encontrar grupos que no sean de forma redonda o convexa.

Agrupamiento Basado en Conectividad (Jerárquico)

Este tipo de agrupamiento, también llamado jerárquico, se basa en la idea de que los objetos más cercanos están más relacionados. Estos algoritmos conectan objetos para formar grupos según su distancia. Un grupo se puede describir por la distancia máxima necesaria para conectar todas sus partes. A diferentes distancias, se forman diferentes grupos. Esto se puede mostrar en un dendrograma, que es un diagrama en forma de árbol.

El agrupamiento jerárquico puede ser:

• Aglomerativo: Empieza con cada objeto como un grupo y los va uniendo.
• Divisivo: Empieza con todos los objetos en un solo grupo y los va dividiendo.

Estos métodos no dan una única división de los datos, sino una jerarquía donde el usuario puede elegir los grupos adecuados. No son muy buenos con el "ruido" (datos que no encajan bien), ya que el ruido puede hacer que los grupos se unan incorrectamente.

• Ejemplos de enlace simple
• 

  Enlace simple en datos Gaussianos. En 35 grupos, al principio el grupo más grande se fragmenta en grupos más pequeños, mientras que todavía está conectado al segundo mayor por el efecto de enlace simple.

• 

  Enlace simple en agrupamiento basado en densidad. Se extrajeron 20 grupos, la mayoría contienen un único elemento, nos podemos percatar entonces que enlace simple no tiene una noción de ruido.

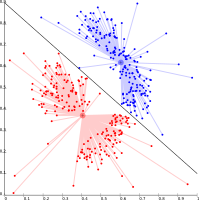
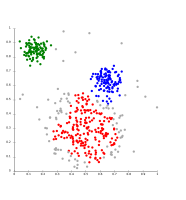
Agrupamiento Basado en Centroide

En este tipo de agrupamiento, los grupos se representan por un punto central llamado centroide. Este centroide no tiene que ser un objeto real de los datos. Si se sabe cuántos grupos (k) se quieren, el algoritmo k-means busca los k centroides y asigna cada objeto al centroide más cercano. El objetivo es que la suma de las distancias de los objetos a sus centroides sea lo más pequeña posible.

El algoritmo de Lloyd, conocido como "k-means", es una forma común de hacer esto. Sin embargo, solo encuentra una solución "localmente" buena, por lo que a menudo se ejecuta varias veces con diferentes puntos de inicio.

La mayoría de los algoritmos k-means necesitan que se les diga cuántos grupos se quieren de antemano, lo cual es una dificultad. Además, estos algoritmos prefieren grupos de tamaño similar, lo que a veces causa divisiones incorrectas en los bordes de los grupos.

K-means tiene propiedades interesantes:

• Divide el espacio de datos en regiones llamadas esquemas de Voronoi.
• Es similar a la clasificación de "k-vecinos más cercanos", por lo que es popular en el aprendizaje automático.

• Ejemplos de agrupamiento con k-means
• 

  K-means separa los datos en esquemas de Voronói, donde se supone igual tamaño para los grupos (no es adecuado para el uso en este caso)

• 

  K-means no puede representar grupos basados en densidad

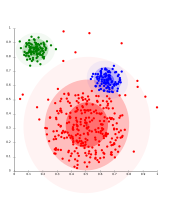
Agrupamiento Basado en Distribuciones

Este modelo está muy relacionado con la estadística. Los grupos se definen como objetos que probablemente pertenecen a la misma distribución estadística. Esto es útil porque así es como a menudo se generan los datos artificiales.

Aunque la base teórica es excelente, estos métodos pueden tener un problema llamado "sobreajuste" (overfitting). Esto significa que el modelo se ajusta demasiado a los datos de entrenamiento y no funciona bien con datos nuevos.

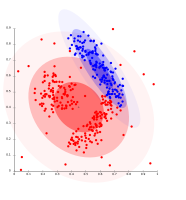
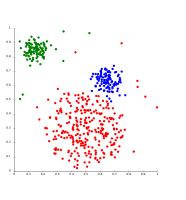
Un método importante es el modelo de mezcla Gaussiana. Aquí, los datos se modelan con un número fijo de distribuciones Gaussianas que se ajustan para clasificar mejor los datos. Los objetos se asignan a la distribución Gaussiana a la que tienen más probabilidad de pertenecer.

Estos algoritmos pueden crear modelos complejos que capturan relaciones entre las características de los datos. Sin embargo, requieren que el usuario sepa qué modelo matemático usar, lo cual no siempre es fácil con datos reales.

• Ejemplos de agrupamiento usando Expectation-Maximization (EM)
• 

  En datos distribuidos con Gaussianas, EM trabaja bien, desde entonces se utilizan Gaussianas para la modelación de grupos.

• 

  Grupos basados en densidad no pueden ser modelados utilizando distribuciones Gaussianas

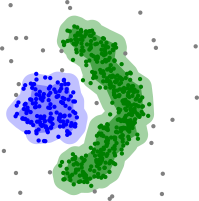
Agrupamiento Basado en Densidad

En este tipo de agrupamiento, los grupos son áreas donde los datos están más densamente agrupados que en el resto del conjunto. Los objetos en áreas dispersas se consideran "ruido" o puntos de frontera.

El método más conocido es DBSCAN. A diferencia de otros métodos, DBSCAN tiene un modelo de grupo bien definido. Se basa en conectar puntos que están dentro de una cierta distancia y cumplen un criterio de densidad (un número mínimo de otros objetos en un radio dado). Un grupo está formado por objetos densamente conectados. Una ventaja de DBSCAN es que es bastante rápido y produce resultados consistentes. OPTICS es una versión mejorada de DBSCAN que no necesita que se elija un valor para el radio y produce un resultado jerárquico.

La principal dificultad de DBSCAN y OPTICS es que necesitan que haya una "caída" en la densidad para detectar los límites de los grupos. No pueden detectar estructuras de grupo internas que son comunes en datos reales.

• Ejemplos de agrupamiento basado en densidad
• 

  Agrupamiento basado en densidad con DBSCAN.

• 

  DBSCAN supone grupos de densidad similar, y puede tener problemas para separar grupos cercanos

• 

  OPTICS es una variante de DBSCAN que maneja densidades diferentes mucho mejor

Desarrollos Recientes

En los últimos años, se ha trabajado mucho para mejorar la velocidad de los algoritmos existentes. Con la necesidad de procesar cada vez más datos (conocidos como big data), se han desarrollado métodos de "pre-agrupamiento" como Canopy. Estos métodos pueden procesar grandes cantidades de datos de manera eficiente, creando una primera división de los datos que luego se puede analizar con métodos más lentos.

Para datos con muchas características (alta dimensionalidad), muchos métodos fallan. Esto llevó a la creación de nuevos algoritmos que se enfocan en agrupar en "subespacios" (donde solo se usan algunas características) y en "agrupamiento de correlación" (que busca grupos donde las características están relacionadas). Ejemplos de estos algoritmos son CLIQUE y SUBCLU.

También se han propuesto sistemas de agrupamiento basados en la información mutua (cuánta información comparten dos conjuntos de datos). Los algoritmos genéticos y los algoritmos de "paso de mensajes" también han llevado a nuevos tipos de algoritmos de agrupamiento.

Otros Métodos

• Esquema algorítmico secuencial básico (BSAS)

¿Cómo Saber si un Agrupamiento es Bueno?

Evaluar los resultados de un agrupamiento es importante para saber qué tan bien se hizo. Hay varias formas de medir qué tan similares son dos agrupamientos.

Evaluación Interna

Cuando se evalúa un agrupamiento basándose solo en los datos que se agruparon, se llama evaluación interna. Estos métodos suelen dar una mejor puntuación a los algoritmos que crean grupos con mucha similitud entre sus miembros y poca similitud entre los grupos. Sin embargo, una puntuación alta en una medida interna no siempre significa que el agrupamiento sea realmente útil. Además, esta evaluación puede favorecer a los algoritmos que usan el mismo modelo de grupo. Por ejemplo, k-means funciona bien con medidas basadas en la distancia.

Por lo tanto, las medidas de evaluación internas son útiles para comparar qué algoritmo funciona mejor en ciertas situaciones, pero no siempre indican que un algoritmo produce resultados más "válidos" que otro.

Algunos métodos comunes para la evaluación interna son:

Índice de Davies–Bouldin

Este índice se calcula comparando la distancia promedio dentro de los grupos con la distancia entre los centroides de los grupos. Un valor bajo en el índice de Davies–Bouldin indica un mejor agrupamiento, con grupos más compactos y bien separados.

Índice de Dunn

El índice de Dunn busca grupos densos y bien separados. Se define como la proporción entre la distancia mínima entre grupos y la distancia máxima dentro de un grupo. Un valor alto en el índice de Dunn es deseable, ya que indica grupos compactos y bien separados.

Coeficiente de Silueta

El coeficiente de silueta compara qué tan cerca está un objeto de su propio grupo con qué tan lejos está de otros grupos. Los objetos con un valor de silueta alto están bien agrupados. Los objetos con un valor bajo pueden ser ruido. Este índice funciona bien con k-means y también se usa para encontrar el número ideal de grupos.

Evaluación Externa

En la evaluación externa, los resultados del agrupamiento se comparan con datos que no se usaron para agrupar, como etiquetas de clases ya conocidas. Estos datos de referencia suelen ser creados por expertos. Así, se puede medir qué tan cerca está el agrupamiento de las clasificaciones predefinidas. Sin embargo, se discute si esto es adecuado para datos reales, ya que las clases pueden tener estructuras internas o contener datos atípicos.

Algunas medidas de calidad que usan criterios externos son:

Medida de Rand

El índice de Rand calcula qué tan similares son los grupos creados por el algoritmo a las clasificaciones de referencia. Se puede ver como el porcentaje de decisiones correctas del algoritmo. Un valor de 1 indica una coincidencia perfecta.

F-Medida

La F-medida equilibra la importancia de los "falsos negativos" (objetos que deberían estar en un grupo pero no lo están). Combina la precisión (cuántos de los objetos agrupados correctamente son realmente del grupo) y el recobrado (cuántos de los objetos del grupo fueron encontrados).

Índice de Jaccard

El índice de Jaccard mide la similitud entre dos conjuntos de datos. Toma un valor entre 0 y 1. Un índice de 1 significa que los dos conjuntos son idénticos, y 0 significa que no tienen elementos en común.

Índice de Fowlkes–Mallows

Este índice calcula la similitud entre los grupos del algoritmo y las clasificaciones de referencia. Cuanto más alto sea el valor, más similares son.

Información Mutua

Es una medida de cuánta información se comparte entre un agrupamiento y una clasificación de referencia. Puede detectar similitudes no lineales.

Matriz de Confusión

Una matriz de confusión es una tabla que ayuda a ver rápidamente los resultados de un algoritmo de clasificación. Muestra qué tan diferente es un grupo del grupo de patrones creado por un experto.

Usos del Agrupamiento en el Mundo Real

El agrupamiento tiene muchas aplicaciones prácticas:

• Biología y Bioinformática
  • Ecología: Para describir y comparar comunidades de organismos en diferentes lugares.
  • Genética: Para agrupar genes con patrones de expresión similares o secuencias parecidas.
  • Genética Humana: Para entender las estructuras de población a partir de datos genéticos.

• Medicina
  • Imágenes médicas: Para diferenciar tipos de tejido en imágenes 3D, como en escáneres PET.
  • Actividad antimicrobiana: Para analizar patrones de resistencia a antibióticos.

• Empresas y Marketing
  • Investigación de mercado: Para dividir a los consumidores en segmentos de mercado y entender sus relaciones.
  • Agrupación de productos: Para organizar todos los productos disponibles en línea en conjuntos únicos.

• Internet (World Wide Web)
  • Análisis de redes sociales: Para reconocer comunidades dentro de grandes grupos de personas.
  • Agrupación de resultados de búsqueda: Para organizar los resultados de búsqueda de manera más útil.
  • Optimización de mapas: Para reducir el número de marcadores en un mapa, haciéndolos más rápidos y claros.

• Informática
  • Segmentación de imagen: Para dividir una imagen digital en regiones distintas.
  • Sistemas de recomendación: Para sugerir nuevos elementos a un usuario basándose en los gustos de otros usuarios en su grupo.
  • Detección de anomalías: Para encontrar datos inusuales o "fuera de lo normal".

• Ciencias Sociales
  • Análisis de delitos: Para identificar áreas con mayor incidencia de ciertos tipos de delitos y dirigir mejor los recursos.
  • Minería de datos educativa: Para identificar grupos de escuelas o estudiantes con características similares.

• Otros Campos
  • Robótica: Para seguir objetos y detectar datos atípicos de los sensores.
  • Química matemática: Para encontrar similitudes estructurales entre compuestos químicos.
  • Climatología: Para encontrar patrones atmosféricos.
  • Geografía física: Para agrupar propiedades químicas en diferentes lugares de muestreo.

Véase también

Proyección de Datos y Preprocesamiento

• Reducción de dimensionalidad
• Análisis de componentes principales
• Escalamiento multidimensional

Otros

• Modelación ponderada de grupos
• Maldición de la dimensión
• Determinando el número de grupos en un conjunto de datos
• Coordenadas paralelas
• Análisis de datos estructurados