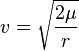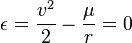Trayectoria parabólica para niños
Una trayectoria parabólica es un tipo especial de camino que sigue un objeto en el espacio, como una nave espacial o un cometa, cuando se mueve alrededor de un planeta o una estrella. Imagina que lanzas una pelota hacia arriba: si la lanzas con la velocidad justa, subirá y subirá, pero nunca volverá a caer. Así es una trayectoria parabólica en el espacio.
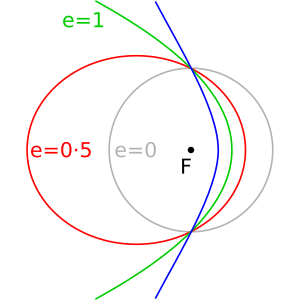
En el estudio de cómo se mueven los objetos en el espacio (conocido como astrodinámica o mecánica celeste), una trayectoria parabólica es una órbita de Kepler donde la forma de la órbita tiene una característica especial llamada excentricidad orbital igual a 1. Esto significa que el camino es una parábola.
Cuando un objeto se aleja de un cuerpo central (como un planeta), se le llama órbita de escape. Si se acerca, se le llama órbita de captura. En una trayectoria parabólica, el objeto se moverá hacia el infinito, y su velocidad respecto al cuerpo central se hará cada vez más pequeña, pero nunca llegará a cero. Por eso, el objeto nunca regresará.
Las órbitas parabólicas son como el punto medio entre las órbitas que se quedan (como las elípticas, donde los objetos giran alrededor de un planeta) y las órbitas que se van muy rápido (como las hiperbólicas, donde los objetos tienen mucha energía y se alejan velozmente).
Contenido
Trayectoria Parabólica: Un Viaje al Espacio
¿Qué es una Trayectoria Parabólica?
Una trayectoria parabólica es un camino que un objeto sigue en el espacio cuando tiene la velocidad exacta para escapar de la atracción gravitatoria de un cuerpo grande, como un planeta o una estrella. Es como un "boleto de ida" al espacio exterior. El objeto se aleja para siempre, pero su velocidad disminuye a medida que se aleja.
Esta trayectoria es el límite entre dos tipos de movimientos:
- Las órbitas elípticas: Son caminos cerrados, como los de los planetas alrededor del Sol. El objeto siempre regresa.
- Las trayectorias hiperbólicas: Son caminos abiertos, donde el objeto tiene mucha velocidad y se aleja rápidamente, sin regresar.
La trayectoria parabólica tiene la energía mínima necesaria para escapar de la gravedad.
La Velocidad en una Trayectoria Parabólica
La velocidad de un objeto que se mueve en una trayectoria parabólica es muy específica. En cualquier punto de su camino, el objeto tiene exactamente la velocidad de escape para esa posición. La velocidad de escape es la velocidad mínima que necesita un objeto para liberarse de la gravedad de un cuerpo.
¿Cómo se calcula la velocidad?
La velocidad orbital (v) de un objeto en una trayectoria parabólica se puede calcular con una fórmula:
Donde:
es la distancia del objeto al centro del cuerpo grande.
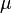es el parámetro gravitacional estándar, que es un número que depende de la masa del cuerpo grande (como un planeta o una estrella).
Esta velocidad es especial porque es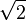 
veces la velocidad que tendría un objeto si estuviera en una órbita circular a la misma distancia.
Por ejemplo, si una nave espacial tiene la velocidad de escape de la Tierra, puede salir de la gravedad terrestre. Pero eso no significa que escape del Sistema Solar. Para escapar del Sol, necesitaría una velocidad de escape mucho mayor. Cerca de la Tierra, su órbita parecería parabólica, pero más lejos, se curvaría en una órbita elíptica alrededor del Sol.
La Energía en una Trayectoria Parabólica
En una trayectoria parabólica, la energía total del objeto en órbita es cero. Esto no significa que no tenga energía, sino que la energía de su movimiento (energía cinética) es exactamente igual a la energía que lo mantiene unido al cuerpo central (energía potencial gravitatoria), pero con signo opuesto. Se cancelan entre sí.
¿Qué significa energía cero?
La ecuación de la conservación de la energía para una trayectoria parabólica se ve así:
Donde:
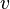es la velocidad del objeto.- es su distancia al cuerpo central.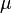
- es el parámetro gravitacional estándar.
Que la energía sea cero significa que el objeto tiene justo la energía necesaria para escapar de la gravedad y llegar al infinito con una velocidad que tiende a cero.
Véase también
En inglés: Parabolic trajectory Facts for Kids
- Órbita de Kepler
- Parábola
