Velocidad de escape para niños
La velocidad de escape es la velocidad mínima que un objeto necesita para alejarse para siempre de un planeta, una estrella o cualquier cuerpo celeste. Imagina que quieres lanzar una nave espacial tan lejos que la gravedad de la Tierra ya no pueda atraerla de vuelta. Esa velocidad inicial que necesitas es la velocidad de escape.
Esta velocidad especial depende de dos cosas principales:
- La masa del cuerpo grande (como un planeta). Cuanto más masivo sea, más fuerte es su gravedad y mayor será la velocidad de escape.
- La distancia desde el centro de ese cuerpo. Cuanto más lejos estés, menos velocidad necesitarás para escapar.
Es importante saber que la velocidad de escape no depende de la masa del objeto que se lanza. ¡Una pequeña roca y una nave espacial gigante necesitan la misma velocidad para escapar de la Tierra!
Por ejemplo, para escapar de la Tierra desde el nivel del mar, necesitas una velocidad de unos 11,19 kilómetros por segundo (km/s). ¡Eso es rapidísimo, como 40.280 kilómetros por hora! Para que te hagas una idea, la velocidad de escape desde la superficie de la Luna es de 2,38 km/s, y desde la superficie del Sol es de 617,7 km/s.
.
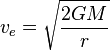Esta fórmula nos ayuda a calcular la velocidad de escape. Aquí, G es la constante de gravitación universal, M es la masa del cuerpo del que quieres escapar, y r es la distancia desde su centro.
Contenido
¿Qué es la Velocidad de Escape?
La velocidad de escape es la velocidad a la que la energía de movimiento de un objeto y su energía de posición (debido a la gravedad) se equilibran. Si un objeto alcanza esta velocidad, no caerá de nuevo a la superficie ni se quedará girando en una órbita cerrada. Simplemente se alejará, haciéndose cada vez más lento, pero nunca se detendrá por completo ni regresará.
Una vez que un objeto alcanza la velocidad de escape, no necesita más empuje. Seguirá alejándose del cuerpo celeste, disminuyendo su velocidad poco a poco, hasta que su velocidad se acerque a cero a una distancia infinita.
¿Cómo se calcula la Velocidad de Escape?
La velocidad de escape a una distancia d del centro de un cuerpo con masa M se calcula con la siguiente fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v_e = \sqrt{\frac{2GM}{d}} Aquí, G es la constante gravitatoria universal (aproximadamente 6.67×10-11 m3·kg-1·s-2). También se puede expresar como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v_e = \sqrt{2gd} , donde g es la aceleración de la gravedad en ese punto.
Por ejemplo, la velocidad de escape desde la superficie de la Tierra es de aproximadamente 11.186 metros por segundo (m/s). Esto es unas 33 veces la velocidad del sonido.
El Concepto de Velocidad de Escape en la Práctica
El concepto de velocidad de escape es muy útil en la astronáutica. Sin embargo, no es la velocidad a la que las naves espaciales se lanzan directamente. Las naves espaciales suelen acelerar gradualmente fuera de la atmósfera. A menudo, primero entran en una órbita alrededor de la Tierra (como la órbita baja terrestre) y luego aceleran desde allí para alcanzar la velocidad de escape.
Desde una órbita baja, la velocidad de escape es un poco menor (unos 11,0 km/s a 200 km de altura). Además, la nave ya tiene una velocidad considerable al estar en órbita (unos 7,8 km/s), lo que reduce la cantidad de velocidad adicional que necesita.
La Idea de Isaac Newton
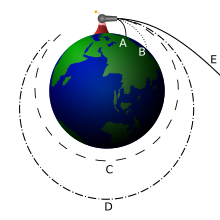
Isaac Newton explicó el concepto de velocidad de escape con un ejemplo muy famoso. Imaginó un cañón disparando proyectiles desde la cima de una montaña muy alta, donde no hay resistencia del aire.
- Si el proyectil se lanza a una velocidad baja, cae a la Tierra.
- Si se lanza a una velocidad específica, entra en órbita circular alrededor de la Tierra. Esta es la primera velocidad cósmica o velocidad orbital.
- Si se lanza más rápido que la velocidad orbital, pero más lento que la de escape, entra en una órbita elíptica.
- Si se lanza exactamente a la velocidad de escape, el proyectil se aleja de la Tierra para siempre, siguiendo una trayectoria que nunca regresa.
- Si se lanza a una velocidad superior a la de escape, también se aleja para siempre, pero con una trayectoria diferente.
Velocidad de Escape y la Altura
La velocidad de escape cambia según la altura a la que te encuentres. Cuanto más lejos estés del centro del planeta, menos velocidad necesitarás para escapar.
Por ejemplo, la velocidad de escape desde la superficie de la Tierra es de 11,19 km/s. Pero a 200 km de altura, es de 11,02 km/s.
También es importante considerar la gravedad de otros cuerpos celestes. La velocidad de escape del Sol a la distancia de la Tierra es de 42,04 km/s. Esto significa que un objeto que escape de la Tierra pero no alcance la velocidad de escape del Sol, se quedará orbitando alrededor del Sol.
Lanzamiento desde un Cuerpo en Rotación
La velocidad de escape que necesitas respecto a la superficie de un planeta que gira depende de la dirección en la que lances el objeto. La Tierra gira, y su superficie en el ecuador se mueve a unos 465 metros por segundo.
Por eso, un cohete lanzado hacia el este desde el ecuador necesita menos velocidad adicional para escapar (unos 10,735 km/s respecto a la superficie). En cambio, si se lanza hacia el oeste, necesitaría más velocidad (unos 11,665 km/s). Por esta razón, los centros de lanzamiento espacial suelen estar cerca del ecuador, como Cabo Cañaveral en Estados Unidos o el Puerto espacial de Kourou en la Guayana Francesa.
Tabla de Velocidades de Escape
Aquí tienes una tabla con las velocidades de escape de algunos cuerpos celestes importantes:
| Objeto | Masa (kg) | Radio (m) | Velocidad de escape (km/s) | con respecto a la Tierra |
|---|---|---|---|---|
| Sol | 2,0 x 1030 | 7,0 x 108 | 617,5 | 55,18 |
| Mercurio | 3,3 x 1023 | 2,4 x 106 | 4,3 | 0,38 |
| Venus | 4,9 x 1024 | 6,1 x 106 | 10,4 | 0,92 |
| Tierra | 6,0 x 1024 | 6,4 x 106 | 11,2 | 1 |
| Luna | 7,3 x 1022 | 1,7 x 106 | 2,38 | 0,21 |
| Marte | 6,4 x 1023 | 3,4 x 106 | 5 | 0,45 |
| Ceres | 9,4 x 1020 | 4,9 x 105 | 0,5 | 0,04 |
| Júpiter | 1,9 x 1027 | 7,1 x 107 | 59,5 | 5,32 |
Galería de imágenes
-
Ilustración del razonamiento de Isaac Newton. Desde la cima de una montaña, un cañón dispara proyectiles con cada vez más velocidad. Los proyectiles A y B caen en tierra. El proyectil C entra en órbita circular y el D en órbita elíptica. El proyectil E se libera de la atracción terrestre.
Véase también
En inglés: Escape velocity Facts for Kids
